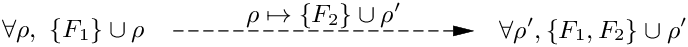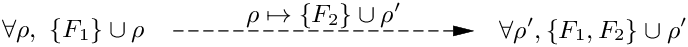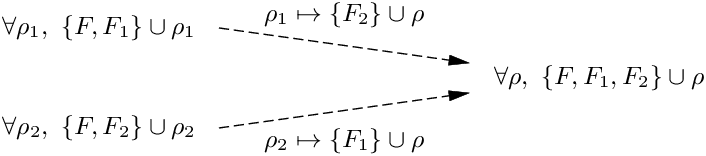Chapter 13 Type and effect systems
Type systems are often applied to programming languages to improve program reliability and clarity. They prevent a number of common programming errors and describe the interfaces of program components.
Type systems provide data integrity guarantees, such as “all elements of an array have the same type” or “a function is only applied to arguments of the expected type”. They can also provide guarantees about the flow of control. For instance, some type systems guarantee termination of programs, while others guarantee that all exceptions that a program can raise are handled within the program, thus avoiding the uncaught exception problem described in section 9.4.
This chapter examines the interactions between type systems and control structures from two perspectives. First, it explores how to extend simple type systems for pure languages to include support for advanced control structures (exceptions, continuations, user-defined effects) while still guaranteeing data integrity. Second, it discusses how type and effect systems can keep track of control effects to ensure safety guarantees regarding control flows, such as the absence of uncaught exceptions or unhandled effects.
13.1 Type systems reminder
Type systems.
A type discipline organizes the values manipulated by programs into types. These types include
- base types such as int for integers, bool for Booleans, string for character strings, etc;
- composite types such as bool → int (functions from Booleans to integers) or string list (homogeneous lists of character strings).
A type system associates types with the values manipulated by a program, and ensures that these types are consistent. For instance, a function of type bool → int can only be applied to Booleans, not strings. Likewise, an integer cannot be applied as if it were a function.
For an expression language such as FUN, a type system is usually defined by a set of typing rules: axioms and inference rules that define a predicate Γ ⊢ e : τ, meaning “under assumptions Γ, the expression e has type τ”. The environment Γ is a partial mapping from variables xi to their types τi.
| | Types:
τ, σ | | ::= | | bool ∣ int ∣ … | | base types |
| | | | ∣ | | σ → τ | | function types
|
|
c ∈ {true, false}
| (const) |
| |
| Γ ⊢ c : bool
| |
|
|
Γ, x : σ ⊢ e : τ
| (abstr) |
| |
| Γ ⊢ λ x . e : σ → τ
| |
|
|
Γ ⊢ e1 : σ → τ Γ ⊢ e2 : σ
| (app) |
| |
| Γ ⊢ e1 e2 : τ
| |
|
|
Γ ⊢ e1 : bool Γ ⊢ e2 : τ Γ ⊢ e3 : τ
| (cond) |
| |
| Γ ⊢ if e1 then e2 else e3 : τ
| |
|
| Figure 13.1: Type algebra and typing rules for the FUN language. |
Figure 13.1 shows the typing rules for the FUN language. Rule (var) states that the type of a variable x is the type associated with x in the typing environment. Rule (const) states that true and false have type bool. Rule (abstr) states that a function λ x . e has type σ → τ if the body e has type τ under the assumption that x has type σ. Rule (app) states that a function of type σ → τ can be applied to an argument of type σ to produce a result of type τ. Finally, rule (cond) states that the conditional if e1 then e2 else e3 has type τ if the condition e1 has type bool and both arms e2 and e3 have type τ.
Type checking.
Although types can be checked dynamically during program execution, stronger guarantees are obtained by checking types statically through compile-time analysis before the program executes. The program analysis in question is called a type checker. It associates types with expressions and variables, and verifies that the typing rules are followed. In simple type systems such as that of FUN, all types can be inferred from an unannotated program. Richer type systems require providing some type information in the program, such as the types of function parameters, i.e. by writing λ x : τ . e instead of just λ x . e.
Type safety
is the property that a well-typed program “does not go wrong” (Milner, 1978), i.e. does not perform an undefined operation such as “true false” (applying the Boolean true to the Boolean false, as if true were a function). Rather, a well-typed program either terminates on a value or diverges safely.
A way to prove type safety, introduced by Wright and Felleisen (1994), involves showing the following two properties of the type system with respect to a reduction semantics for the language:
- Preservation (of types by reductions): if ⊢ e : τ and e → e′, then ⊢ e′ : τ.
- Progress (of well-typed programs): if ⊢ e : τ, then either e is a value or e can reduce.
See Pierce (2002), sections 8.3 and 9.3, for more details and for a proof of type safety for FUN along these lines.
13.2 Simple types for advanced control structures
Exceptions.
The main issue with typing exceptions is ensuring that the code that raises an exception and the code that catches it agree on the type of the exception value. One simple solution is to use a fixed type exn of exception values. This leads to the following typing rules:
|
Γ ⊢ e : exn
|
|
| Γ ⊢ raise e : τ
|
|
|
Γ ⊢ e1: τ Γ, x : exn ⊢ e2: τ
|
|
| Γ ⊢ try e1 with x → e2 : τ
|
|
The expression raise e never produces a value, so it has all possible types τ. Alternatively, in a polymorphic type system (section 13.3), raise can be viewed as a predefined function with the polymorphic type ∀ α, exn → α.
In OCaml and other functional languages from the ML family, the exn type is an extensible data type, and declaring an exception amounts to adding a constructor to the type exn. For instance, the declaration
exception Error of string
is equivalent to
type exn += Error of string
and introduces the constructor Error with type string → exn.
In Java and other object-oriented languages, the role of the exn type is played by the Throwable class. Declaring an exception amounts to defining a subclass of Throwable.
Type safety for exceptions
can be proved directly using a preservation-and-progress argument and the reduction semantics for exception from section 9.2. (See Wright and Felleisen (1994) for a proof.) A simpler way to show type safety is to observe that the ERS (exception-returning style) transformation of section 9.3 not only preserves semantics, but also preserves typing, in the following sense:
| if
Γ ⊢ e : τ
then
| | ⊢ ℰ(e) : | | + exn
|
We write τ for the type of a value of type τ after ERS transformation, namely:
|
| | = ι for all base types ι (bool, exn, etc.)
| | | | | | | | | |
| | | | | | | | | | |
|
Consequently, if e is a closed program of base type ι, then its ERS transform ℰ(e) has type ι + exn and either diverges or terminates with a value of type ι + exn. This means that e either diverges, or terminates normally with a value of type ι, or terminates on an uncaught exception. The typing is safe to the extent that e cannot “go wrong”, but it does not prevent e from raising an exception and forgetting to handle it.
Effect handlers.
The simple typing of exceptions shown above can easily be extended to user-defined effects and effect handlers, guaranteeing type safety but not the absence of unhandled effects. The main difference is that, unlike raising an exception, performing an effect can return a value.
As in OCaml, we introduce the parameterized type τ eff of effects that return a value of type τ. Declaring an effect amounts to extending the type eff with a new constructor, as shown in section 10.1. The typing rules for the perform and handle constructs of section 10.5 are as follows:
|
Γ ⊢ e : τ eff
|
|
| Γ ⊢ perform e : τ
|
|
|
| |
Γ ⊢ e: σ Γ⊢ eret : σ → τ Γ⊢ eeff : α eff → (α → τ) → τ for all types α
|
|
| Γ ⊢ handle e with eret, eeff : τ
|
|
perform takes an effect of type τ eff as argument and returns a result of type τ. In handle e with eret, eeff, the normal handler eret has type σ → τ, since it receives the value of e, of type σ, as argument, and produces the return value of the handle construct, of type τ. The effect handler eeff has a more subtle type. It must accept any effect of type α eff as first argument; hence the quantification “for all types α”. The second argument is a delimited continuation, expecting an argument of type α (which is the return value for the corresponding perform) and producing a result of type τ. The result of eeff has type τ, the type of the handler’s result.
The typing above is that of a “deep” handler. For a “shallow” handler, the continuation has type α → σ instead of α → τ because it is not covered by the handler and therefore produces values of the same type σ as the handled computation e.
Call-with-current-continuation (callcc). The callcc and throw operators of section 8.2 can be typed as follows:
|
Γ, k : τ cont ⊢ e : τ
|
|
| Γ ⊢ callcc (λ k . e) : τ
|
|
|
Γ ⊢ e1 : τ cont Γ ⊢ e2 : τ
|
|
| Γ ⊢ throw e1 e2 : σ
|
|
The type τ cont is the type of continuations that expect an argument of type τ. In the Scheme presentation of call/cc, where continuations are functions that never return and the throw operator is simply function application, τ cont would be a function type such as τ → ∀ α . α. (Since continuations do not return, any type can be assumed for their results, as in the case of exception raising.)
In the presentation above, throw is an operator that applies a continuation of type τ cont to an argument of type τ. In callcc (λ k . e), k is bound to a τ cont continuation, where τ is the type of both e and the whole callcc expression.
In SML/NJ, callcc and throw are not language constructs but predefined library functions with polymorphic types:
|
| | callcc | : ∀ α, (α cont → α) → α | | | | | | | | | |
|
throw | : ∀ α β, α cont → α → β
| | | | | | | | | |
|
Type safety for callcc.
We can show type safety for callcc and throw using the reduction semantics of section 8.4 and a proof by preservation and progress (Wright and Felleisen, 1994). An alternative proof of type safety uses the fact that the call-by-value CPS transformation of section 6.5 preserves types, in the following sense:
| if
Γ ⊢ e : τ
then
| | ⊢ 𝒞(e) : ( | | → R) → R
|
Here, R is the “result type”, i.e. the type of the whole program,
and τ is the type of a value of type τ after CPS transformation:
In particular, if p is the whole program, with ⊢ p : R and R is a base type, we have ⊢ 𝒞(p) (λ x . x) : R. This guarantees that the transformed program 𝒞(p) applied to the initial continuation λ x . x executes without going wrong.
Multi-prompt delimited continuations.
Control operators for delimited continuations are easy to type-check as long as the “prompts” that delimit continuations have fixed, statically-known types. This is not an issue when multiple prompts are supported because we can create a new prompt for each type of continuation needed. Following Gunter et al. (1995), we introduce a type τ prompt of prompts that can delimit computations of type τ, along with three predefined operations:
|
| | new_prompt | : ∀ α, unit → α prompt
| | | | | | | | | |
|
delim | :
∀ α, α prompt → (unit → α) → α
| | | | | | | | | |
|
capture | :
∀ α β, α prompt →
((β → α) → α) → β
| | | | | | | | | |
|
delim p f, written set p f in Gunter et al. (1995), evaluates f() with the prompt p set to the program point where the delim expression returns. The type of the prompt, α prompt, must agree with the type α of f().
capture p (λ k . e), also written cupto p (λ k . e), captures the delimited continuation that extends from the current program point to the nearest delimiter delim p for the same prompt p. It binds the continuation to k, returns to the delim p point, and then evaluates e. If the capture expression has type β and the prompt p has type α prompt, then the nearest delimiter delim p has type α. Therefore, the delimited continuation has type β → α. If e returns normally, its value becomes the value of the delim expression. Therefore, it must have type α.
Fine-grained typing of single-prompt delimited continuations.
Some control operators for delimited continuations only support one prompt. This is the case for control/prompt (Felleisen, 1988) and shift/reset (Danvy and Filinski, 1990). In this case, it is unrealistic to use a fixed type for the prompt. Instead, Danvy and Filinski (1989) describe a type system for shift/reset that keeps track not only of the types of the current variables and of the current expression, but also of the type of the prompt. Since shift expressions can move the prompt and change its type, two types are recorded for the prompt, one before and one after the execution of the expression. The typing relation thus becomes
where τ is the type of the value returned by e,
α is the original result type before e is evaluated,
and β is the new result type after e is evaluated. The “result type” is the type of the enclosing evaluation context, i.e. the type of the nearest prompt. One way to understand the two result types α and β is to observe that the delimited CPS transformation of e has type
(τ → α) → β .
Function types σ → τ become σ ; α → τ ; β in order to keep track of the result types before and after the function application. Once transformed to CPS, a function with the type above will have type σ → (τ → α) → β.
|
(Γ, x : σ); α ⊢ e : τ; β
|
|
| Γ; δ ⊢ λ x . e : (σ; α →
τ;β); δ
|
|
|
Γ; δ ⊢ e1 : (σ; α → τ; ε); β
Γ; ε ⊢ e2: σ; δ
|
|
| Γ; α ⊢ e1 e2: τ;β
|
|
The typing rule for function applications reflects a left-to-right evaluation order in the evolution of the result type: from β to δ when evaluating e1, then from δ to ε when evaluating e2, and finally from ε to α when the function is applied.
|
Γ; σ ⊢ e : σ; τ
|
|
| Γ; α ⊢ reset e : τ; α
|
|
|
(Γ, k : τ; δ → α; δ); σ ⊢ e : σ;β
|
|
| Γ; α ⊢ shift (λ k . e) : τ; β
|
|
The reset delimiter installs a new result type σ, which is also the type of the delimited expression e, and ensures that the current result type α remains unchanged during the evaluation of reset e.
The shift operator captures the continuation that extends from the end of the evaluation of the shift expression (type τ) to the delimiter expecting a result of type α.
Note that a continuation does not move the prompt; therefore, it is a function from τ to α with the same type δ for the two result types.
13.3 Issues with parametric polymorphism
Parametric polymorphism.
Some FUN expressions have many different types. For example, λ x . x has type τ → τ for any type τ. To express all of these types at once, we can introduce type variables α and polymorphic types ∀ α, τ.
| | Types:
τ, σ | | ::= | | bool ∣ int ∣ … | | base types |
| | | | ∣ | | σ → τ | | function types |
| | | | ∣ | | α | | type variables |
| | | | ∣ | | ∀ α , τ | | polymorphic types
|
Then, λ x . x has type ∀ α, α → α, and can be used with any instance of this polymorphic type, namely any type τ → τ for some type τ.
The following two typing rules capture this style of parametric polymorphism:
|
Γ ⊢ e : τ α not free in Γ
| (gen) |
| |
| Γ ⊢ e : ∀ α, τ
| |
|
|
Γ ⊢ e : ∀ α, τ
| (inst) |
| |
| Γ ⊢ e : τ [α := σ]
| |
|
For type inference reasons, languages such as Haskell, OCaml and SML limit the (gen) rule to let-bound expressions. This is irrelevant to the following discussion.
The polymorphic reference problem.
Parametric polymorphism using the rules (gen) and (inst) above is perfectly type-safe for pure functional languages. However, it is unsound in the presence of mutable data structures such as references in ML-style languages. Consider:
let f = ref (fun x -> x) in
f := (fun x -> x + 1);
!f "hello"
If we give f the type ∀ α, (α → α) ref, as allowed by rule (gen), we can first use f with type (int → int) ref, storing the successor function in f, and then use f with type (string → string) ref, reading back the successor function with type string → string. However, the program goes wrong when evaluating "hello" + 1.
To avoid this unsoundness, many restrictions on parametric polymorphism have been proposed. The one that is used in SML 97 and in OCaml (with some extensions) is the value restriction: the only expressions that can have their types generalized are syntactic values, namely constants, variables, function abstractions, and constructors applied to values. This is captured by the following restricted rule for type generalization.
| | Syntactic values: v | | ::= | | c ∣ x ∣ λ x . e ∣ C v1 ⋯ vn
| |
|
Γ ⊢ v : τ α not free in Γ v syntactic value
| (gen-val) |
| |
| Γ ⊢ v : ∀ α , τ
| |
|
With the value restriction, the reference f in the example above cannot receive a polymorphic type, since ref (fun x -> x) is not a syntactic value. It can only receive a monomorphic type such as (int → int) ref or (string → string) ref, but it cannot be used with both types. However, almost all useful polymorphic definitions are function definitions, such as
let compose f g = fun x -> f (g x)
Those definitions are syntactic values; they can still be given polymorphic types.
The polymorphic callcc problem.
The problem of parametric polymorphism described above was believed to be specific to references and other mutable data structures until 1991. That year, Harper and Lillibridge demonstrated a similar issue involving callcc but no mutable data. Consider:
type 'a attempt = { current: 'a; retry: 'a -> unit }
let r =
callcc (fun k ->
let rec retry f =
throw k { current = f; retry = retry } in
{ current = (fun x -> x); retry = retry }) in
r.current "hello";
r.retry (fun x -> x + 1)
In this example, callcc is used to backtrack the definition of r and to execute r.current "hello" twice, with two different functions r.current. More precisely, callcc first returns normally, binding r.current to the identity function. The application r.current "hello" is safe. Next, r.retry is called, the captured continuation k is restarted, and callcc returns again, binding r.current to the successor function. The application r.current "hello", then, goes wrong while evaluating "hello" + 1.
Without the value restriction, this example is well-typed. Using the types for callcc and throw from section 13.2, the expression that defines r has type (α → α) attempt for any type α. Rule (gen) allows us to give r the polymorphic type ∀ α, (α → α) attempt, making both calls r.current "hello" and r.retry (fun x -> x + 1) well-typed. With the value restriction, the type of r remains monomorphic since the expression callcc (…) is not a value. Thus, the example is ill-typed.
The CPS transformation sheds some light on this phenomenon. In the presence of the unrestricted (gen) rule, type preservation for the CPS transformation requires that if e : τ and 𝒞(e) : (τ → R) → R, then 𝒞(e) also has type ((∀ α, τ) → R) → R. This is not true for applications of callcc, as shown by counterexamples similar to the one above (Harper and Lillibridge, 1993). However, this is true if e is a syntactic value v, in which case 𝒞(e) = λ k . k Ψ(v), where Ψ(v) is a syntactic value of type τ, and also of type ∀ α,τ by rule (gen-val).
13.4 A simple type and effect system for checked exceptions
Type and effect systems
extend conventional type systems with the ability to track the effects that may be performed when evaluating an expression. They were introduced by Lucassen and Gifford (1988) in the context of the FX-87 language, as a way to detect subexpressions that can be evaluated in parallel because their effects do not interfere. Type and effect systems can also be used to improve software reliability, by demonstrating the absence of undesirable effects such as uncaught exceptions.
A type and effect system defines a four-place typing relation Γ ⊢ e : τ ! ϕ, which means that, under assumptions Γ, the expression e has the value type τ and the effect type ϕ. Value types describe the values returned by expressions. They are the familiar type expressions that describe sets of values, such as int or bool → bool. Effect types describe the effects that can occur during the evaluation of e. Initially, we will consider only two effect types: “pure” if the evaluation of e performs no effects whatsoever, and “impure” if its evaluation may perform some effects. More precise effect types are discussed in section 13.5.
Tracking purity with a type and effect system.
We will now present a simple type and effect system for FUN plus exceptions. The value types and effect types are as follows:
| | Value types:
τ, σ | | ::= | | bool ∣ … | | base types |
| | | | ∣ | | exn | | the type of exceptions |
| | | | ∣ | | σ –[ϕ]→ τ | | function type (ϕ = latent effect)
|
| | Effect types:
ϕ | | ::= | | 0 | | pure computation (no exceptions) |
| | | | ∣ | | 1 | | impure computation (may raise an exception)
|
A defining feature of effect systems is the enriched function type σ –[ϕ]→ τ, where σ is the type of the argument values, τ the type of the result values, and ϕ the latent effect of the function, i.e. the effects that may be performed when the function is applied. This is evident in the typing rule for function abstractions:
|
Γ, x : σ ⊢ e : τ ! ϕ
| (abstr) |
| |
| Γ ⊢ λ x . e : σ –[ϕ]→ τ ! 0
| |
|
The effect ϕ of the body e of the function is the latent effect of the function abstraction λ x . e. The λ x . e expression itself is pure: it is already a value, hence its evaluation cannot perform effects.
|
Γ(x) = τ
| (var) |
| |
| Γ ⊢ x : τ ! 0
| |
|
|
c ∈ {true, false}
| (const) |
| |
| Γ ⊢ c : bool ! 0
| |
|
Like function abstractions, variables and constants are considered pure.
|
Γ ⊢ e : τ ! 0
| (sub) |
| |
| Γ ⊢ e : τ ! 1
| |
|
Any pure expression can also be viewed as impure, if necessary to satisfy the context in which it occurs.
|
Γ ⊢ e1 : bool ! ϕ Γ ⊢ e2 : τ ! ϕ Γ ⊢ e3 : τ ! ϕ
| (cond) |
| |
| Γ ⊢ if e1 then e2 else e3 : τ ! ϕ
| |
|
A conditional expression if e1 then e2 else e3 is pure only if e1, e2, and e3 are pure. If one of these expressions can raise an exception, so can the conditional. We capture this constraint by assigning the same effect ϕ to the three expressions and to the conditional. Since a pure expression can always be given effect 1 using rule (sub), the rule (cond) correctly handles cases where some but not all of the three expressions are pure.
|
Γ ⊢ e1 : σ –[ϕ]→ τ ! ϕ Γ ⊢ e2 : σ ! ϕ
| (app) |
| |
| Γ ⊢ e1 e2 : τ ! ϕ
| |
|
Similarly, a function application e1 e2 is pure only if e1 and e2 are pure and the function obtained by evaluating e1 has latent effect 0. We capture this constraint by assigning the same effect ϕ to e1, e2, the latent effect of the function, and the application e1 e2.
|
Γ ⊢ e : exn ! ϕ
| (raise) |
| |
| Γ ⊢ raise e : τ ! 1
| |
|
Raising an exception is an effect. Therefore, raise e is an impure expression, with an effect type of 1.
|
Γ ⊢ e1 : τ ! 1 Γ, x : exn ⊢ e2 : τ ! ϕ
| (try) |
| |
| Γ ⊢ try e1 with x → e2 : τ ! ϕ
| |
|
|
Γ ⊢ e1 : τ ! 0 Γ, x : exn ⊢ e2 : τ ! ϕ2
| (try-pure) |
| |
| Γ ⊢ try e1 with x → e2 : τ ! 0
| |
|
The exception handler try e1 with x → e2 catches all exceptions that e1 can raise. The only exceptions that can escape are those raised by e2. Therefore, the effect of e1 is ignored, and the effect of the try is the effect of e2. Additionally, if e1 can be typed with an effect of 0, then we know that e1 is pure. In this case, e2 is never evaluated and the entire try expression is pure.
Type safety and checked exceptions.
The type and effect system above can be used to prove the absence of uncaught exceptions: if a program p can be typed with effect 0 (i.e. ⊢ p : τ ! 0), the execution of p cannot stop on an uncaught exception; all exceptions possibly raised by p are handled within p. This can be proved by first showing the preservation property:
| Preservation: if ⊢ e : τ ! ϕ and
e → e′ then ⊢ e′ : τ ! ϕ |
Now, assume that ⊢ p : τ ! ϕ and that p stops on an uncaught exception, meaning that p →* raise v for some exception value v. By preservation, ⊢ raise v : τ ! ϕ. By the (raise) typing rule, ϕ must be 1. It follows that if ⊢ p : τ ! 0, then p cannot stop on an uncaught exception.
A limitation of simple types and effects. According to the rules (abstr) and (sub), a pure function such as λ x . x + 1 can have any latent effect ϕ. However, if ϕ = 0, the function can be only called in a pure context; if ϕ = 1, it can be only called in an impure context. This can be limiting. Consider:
let use_pure (f: int –[0]→ int) = f 2 + f 3
let use_impure (f: int –[1]→ int) = if ... then f 4 else raise E
Then, the function λ f . use_pure f + use_impure f is ill-typed: either f is given type int –[0]→ int and the call to use_impure is ill-typed, or f is given type int –[1]→ int and the call to use_pure is ill-typed.
This simplified example shows that we need type and effect systems that support polymorphism over the latent effects of functions. This can be achieved through subtype polymorphism or parametric polymorphism, as explained in sections 13.5 and 13.6.
13.5 Subtyping over effect types
A lattice of effects.
Effect types are naturally ordered from “having fewer effects” to “having more effects”. We use the symbol ⊆ to represent the partial order between effect types. Purity, i.e. the absence of effects, is the smallest element in this partial order.
For example, the effect types ϕ ::= 0 ∣ 1 of section 13.4 are ordered by 0 ⊆ 1 and have 0 as the smallest element.
In many type and effect systems, effect types ϕ are finite sets {F1, …, Fn} of atomic effects, ordered by set inclusion. The empty set ∅ signifies the absence of effects. Atomic effects F can take many forms:
- Classes of effects, such as
F ::= div ∣ state ∣ exn ∣ ctrl.
These effects capture the use of partiality (div), mutable state (state), exceptions (exn), or control operators (ctrl). The effect type {state;exn} denotes a computation that can use both mutable state and exceptions.
- Names of exceptions or user-defined effects. For example, the effect type {E1; E2} could denote an expression that can raise the exceptions named E1 or E2, regardless of the arguments carried by these exception names.
- Names and types, such as E(τ) for an exception E carrying an argument of type τ, or F(σ ↠ τ) for a user-defined effect F with argument type σ and result type τ.
- Names, types and regions for fine-grained analysis of mutable state. For example, Talpin and Jouvelot (1994) use atomic effects init(ρ, τ), read(ρ, τ) and write(ρ,τ) to track allocation, reading and assignment of a reference containing a value of type τ in the memory region ρ.
From subsumption to subtyping.
The typing rule (sub) of the simple type and effect system of section 13.4 says that a pure expression can always be considered as impure. More generally, an expression that has the effect ϕ can always be considered to have a larger effect ϕ′ ⊇ ϕ:
|
Γ ⊢ e : τ ! ϕ ϕ⊆ ϕ′
| (sub1) |
| |
| Γ ⊢ e : τ ! ϕ′
| |
|
As shown by the example at the end of section 13.4, this typing rule is not flexible enough. Sometimes, we would like to “enlarge” the latent effect of a function, for example to use a pure function in a context that expects an impure function. To this end, we introduce a subtype relation τ <: τ′ between value types τ, τ′, and we use the following stronger rule:
|
Γ ⊢ e : τ ! ϕ τ<: τ′ ϕ⊆ ϕ′
| (sub) |
| |
| Γ ⊢ e : τ′ ! ϕ′
| |
|
The subtyping relation <: is defined by
|
σ′ <: σ ϕ⊆ ϕ′ τ<: τ′
|
|
| σ –[ϕ]→ τ <: σ′ –[ϕ′]→ τ′
|
|
Note the contravariance σ′ <: σ in the argument types, as opposed to the covariance τ <: τ′ in the result types and ϕ ⊆ ϕ′ in the latent effects. For example, we have
| int –[0]→ int <: int –[1]→ int |
since a pure function can be viewed as impure, and also
| int –[1]→ (int –[0]→ int)
<:
int –[1]→ (int –[1]→ int) |
since a function returning a pure function can be viewed as a function returning an impure function, but
| (int –[1]→ int) –[1]→ int
<:
(int –[0]→ int) –[1]→ int |
since a function taking an impure function as its argument can be restricted to taking only pure functions as its argument.
Using the (sub) rule, it is now possible to apply the higher-order function use_impure : (int –[1]→ int) –[1]→ int to a pure function f: int –[0]→ int. Either f is used with the supertype int –[1]→ int, or use_impure is used with the supertype (int –[0]→ int) –[1]→ int.
13.6 Row polymorphism for effect types
A limitation of subtyping for higher-order functions.
Consider an internal iterator over a data structure, such as the map iterator for lists.
let rec map f l =
match l with [] -> [] | x :: l -> f x :: map f l
By itself, map has no effects: the effects performed by map f l are those performed by f. Therefore, we expect map f to be typed as a pure function if f is pure, and as an impure function otherwise:
|
| | map | : (σ –[0]→ τ) –[0]→ (σ list –[0]→ τ list)
| | | | | | | | | (i) |
|
map | : (σ –[1]→ τ) –[0]→ (σ list –[1]→ τ list)
| | | | | | | | | (ii) |
|
However, neither of these two types is subtype of the other, and their common subtype (σ –[1]→ τ) –[0]→ (σ list –[0]→ τ list) is not a valid type for map. Consequently, we would need two copies of the definition of map: map_pure, which is given type (i) above, and map_impure, which is given type (ii) above.
Parametric polymorphism over effect types
provides a better solution to this problem. We can add effect type variables ρ to effect types. These variables can be used, generalized, and instantiated just like the value type variables α in section 13.3. In particular, we can give the map function a highly polymorphic type:
| map : ∀ α β ρ,
(α –[ρ]→ β) –[0]→ (α list –[ρ]→ β list)
|
This type makes the map function generic not only in the argument type α and the result type β of the function being mapped, but also in its latent effect ρ. Types (i) and (ii) above are instances of this polymorphic type, taking α = σ, β = τ, and ρ = 0 or ρ = 1 as appropriate.
Parametric polymorphism and sets of effects. Can we reap the benefits of effect polymorphism for effect types richer than “pure or impure”, such as the sets of atomic effects described in section 13.5? Consider for example the function
let use f x = if x < 0 then raise Error else f x
Ideally, the type of use f x would state that this expression can raise any exception that f can raise, plus the Error exception. To this end, we introduce extensible sets of atomic effects {F1, …, Fn} ∪ ρ, which denotes the effects F1, …, Fn plus all the effects from the effect variable ρ. The desired type for use would then be:
| use : ∀ α ρ, (int –[ρ]→ α) –[0]→ int –[{Error} ⋃ ρ]→ α |
Extensible sets have interesting, subsumption-like properties. By instantiating the extension variable ρ, we can add more atomic effects to the set:
Similarly, by instantiating the extension variables of two sets, we can take their union:
Unlike the subtyping relation of section 13.5, which is contravariant in function argument position, this notion of subsumption based on effect variable instantiation is covariant in all positions. Some type and effect systems, such as the one of section 13.7, lack a subtyping rule and rely exclusively on effect variable instantiation to express subsumption.
Rows and row polymorphism.
Rows of types were introduced by Wand (1987) and further developed by Rémy (1989) to support precise typing and type inference for records and objects. They provide a rigorous formulation of the idea of extensible sets of effects. A distinctive feature of rows is that they can express the absence of an element in such a set, not just its presence.
| | Rows:
ϕ | | ::= | | ρ | | row variable |
| | | | ∣ | | ∅ | | empty row |
| | | | ∣ | | F: π; ϕ | | ϕ plus element F with presence π
|
| | Presence:
π | | ::= | | θ | | presence variable |
| | | | ∣ | | Abs | | absent |
| | | | ∣ | | Pre(τ) | | present with type τ
|
Rows are treated modulo permutation and absorption:
|
| | F1: π1; F2 : π2; ϕ | = F2: π2; F1 : π1; ϕ
| | | | | | | | | (permutation) |
|
F: Abs; ∅ | = ∅
| | | | | | | | | (absorption) |
|
By using a kind system for the row variables ρ, we can ensure that rows never contain duplicate elements F, thus ruling out the possibility of contradictory information on an element F, and making unification well-defined. Using rows instead of extensible sets, the type for the function use above is
| use : ∀ α ρ θ,
(int –[Error: θ; ρ]→ α) –[0]→
int –[Error: Pre(unit); ρ]→ α |
The function f passed to use may or may not have the Error effect, as expressed by the θ presence variable. However, the full application of use definitely has the Error effect, as expressed by the Pre(unit) presence declaration; and it has all the other effects ρ that its argument f has.
13.7 A polymorphic type and effect system for algebraic effects
We will now develop a type and effect system for the small language of algebraic effects and handlers of section 12.7. This system aims to ensure type safety and to prevent “unhandled effect” errors. It is based on Hillerström and Lindley (2016), represents effect types as rows, and uses row polymorphism but no subtyping. Below is the syntax of the language, slightly simplified from section 12.7:
| | Values:
v | | ::= | | x ∣ c ∣ λ x. M
| |
| | Computations:
M, N | | ::= | | v v′ | | application |
| | | | ∣ | | if v then M else N | | conditional |
| | | | ∣ | | val v | | trivial computation |
| | | | ∣ | | do x ⇐ M in N | | sequencing of computations |
| | | | ∣ | | perform F(v) | | performing an effect |
| | | | ∣ | | with H handle M | | handling an effect
|
| | Handlers:
H | | ::= | | { val(x) → Mval; | |
| | | | | | F1(x; k) → M1; | |
| | | | | | ⋮ | |
| | | | | | Fn(x; k) → Mn }
| |
Here are the value types and the effect types:
| | Value types:
τ, σ | | ::= | | α | | variable |
| | | | ∣ | | int ∣ bool | | base types |
| | | | ∣ | | σ –[ϕ]→ τ | | function types |
| | | | ∣ | | ∀ α,τ ∣
∀ ρ,τ ∣
∀ θ,τ | | polymorphism
|
| | Effect types:
ϕ | | ::= | | ρ ∣ ∅ ∣ F: π; ϕ | | rows of effects F
|
| | Presence types:
π | | ::= | | θ ∣ Abs ∣ Pre(σ ↠ τ)
| |
The notation F: Pre(σ ↠ τ) in an effect type denotes the presence of an effect named F carrying an argument of type σ and producing a result of type τ. Note that, unlike in section 13.2, there is no extensible datatype τ eff for effect values. Effects F are just names and do not need to be defined and given a fixed type in advance. It is the Pre(σ ↠ τ) information carried by effect types that ensures type agreement between the performer and the handler of an effect.
Typing of values: Γ ⊢ v : τ
|
c ∈ {true, false}
| (const) |
| |
| Γ ⊢ c : bool
| |
|
|
Γ, x : σ ⊢ M : τ ! ϕ
| (abstr) |
| |
| Γ ⊢ λ x . M : σ –[ϕ]→ τ
| |
|
Typing of computations: Γ ⊢ M : τ ! ϕ
|
Γ ⊢ v1 : σ –[ϕ]→ τ Γ ⊢ v2 : σ
| (app) |
| |
| Γ ⊢ v1 v2 : τ ! ϕ
| |
|
|
Γ ⊢ v : bool Γ ⊢ M : τ ! ϕ Γ ⊢ N : τ ! ϕ
| (cond) |
| |
| Γ ⊢ if v then M else N : τ ! ϕ
| |
|
|
| |
Γ ⊢ v : τ | (ret) |
| |
| Γ ⊢ val v : τ ! ϕ | |
|
|
Γ ⊢ M : σ ! ϕ Γ, x : σ ⊢ N : τ ! ϕ | (bind) |
| |
| Γ ⊢ do x ⇐ M in N : τ ! ϕ | |
|
|
Γ ⊢ v : σ | (perform) |
| |
| Γ ⊢ perform F(v) : τ ! | ⎛
⎝ | F : Pre(σ ↠ τ); ϕ | ⎞
⎠ |
| |
|
|
Γ ⊢ M : σ ! ψ Γ⊢ H : σ ! ψ ⇒ τ ! ϕ
| (handle) |
| |
| Γ ⊢ with H handle M : τ ! ϕ | |
|
Plus: rules for generalization and instantiation of α, ρ, θ type variables.
Typing of handlers: Γ ⊢ H : σ ! ψ ⇒ τ ! ϕ
|
ψ = F1 : Pre(σ1 ↠ τ1) ; …; Fn : Pre(σn ↠ τn) ; ω ϕ= F1 : π1; …; Fn : πn; ω |
| Γ, x : σ ⊢ Mval : τ ! ϕ Γ, x : σi, k : τi –[ϕ]→ τ ⊢ Mi : τ ! ϕ
for i=1,…,n
| (deep) |
| |
| Γ ⊢ { val(x) → Mval; F1(x, k) → M1; …; Fn(x,k) → Mn} : σ ! ψ ⇒ τ ! ϕ
| |
|
| Figure 13.2: A type and effect system for a language with algebraic effects and handlers. |
Figure 13.2 lists the typing rules for values, for computations, and for handlers. Since “values are; computations do” (P. Blain Levy), a value has only a value type (Γ ⊢ v : τ) while a computation has both a value type and an effect type (Γ ⊢ M : τ ! ϕ). Handlers are typed as transformers of value/effect types (Γ ⊢ H : σ ! ψ ⇒ τ ! ϕ).
The rules for values are unsurprising. In rule (abstr), the effect of the function body M becomes the latent effect of the function abstraction λ x . M.
A value v can be used as a trivial computation val v with any effect type ϕ of our choice (rule (ret)). Often, ϕ is ∅ or an effect variable ρ, to express the absence of an effect, but other choices may be needed to satisfy other typing constraints. Rule (bind) is an example of such a constraint: the same effect ϕ must account for the two computations M and N that are being sequenced by do x ⇐ M in N.
The rules for applications (app) and conditionals (cond) are simpler versions of the corresponding rules in section 13.4.
The first rule that uses nontrivial row types is the one for performing an effect:
|
Γ ⊢ v : σ | (perform) |
| |
| Γ ⊢ perform F(v) : τ ! | ⎛
⎝ | F : Pre(σ ↠ τ); ϕ | ⎞
⎠ |
| |
|
The effect type for perform F(v) must be nonempty and contain the effect F as present with the type σ ↠ τ, where σ is the type of the argument v, and τ the type of the result of the perform expression. The types σ and τ are not attached to F by a prior declaration of F: different perform F expressions can use different types.
The rule for handled computations with H handle M is straightforward, but the rule for handlers H is not:
|
Γ ⊢ M : σ ! ψ Γ⊢ H : σ ! ψ ⇒ τ ! ϕ
| (handle) |
| |
| Γ ⊢ with H handle M : τ ! ϕ | |
|
|
ψ = F1 : Pre(σ1 ↠ τ1) ; …; Fn : Pre(σn ↠ τn) ; ω ϕ= F1 : π1; …; Fn : πn; ω |
| Γ, x : σ ⊢ Mval : τ ! ϕ Γ, x : σi, k : τi –[ϕ]→ τ ⊢ Mi : τ ! ϕ
for i=1,…,n
| (deep) |
| |
| Γ ⊢ { val(x) → Mval; F1(x, k) → M1; …; Fn(x,k) → Mn} : σ ! ψ ⇒ τ ! ϕ
| |
|
A handler transforms a value/effect type σ ! ψ into another τ ! ϕ. The rows “before” (ψ) and “after” (ϕ) share a common suffix ω, which describes the effects other than the effects F1, …, Fn that are being handled. The effect Fi must be present in ψ, with a type σi ↠ τi, while it can have any presence πi of our choice in ϕ. If the cases Mval, M1, …, Mn of the handler do not perform Fi, we can take πi = Abs, indicating that the effect Fi was handled for good.
The cases of the handler must all have the same type τ ! ϕ. The value case val(x) → Mval is typed assuming x: σ, where σ is the value type of the handled expression. Each effect case Fi(x, k) → Mi is typed assuming x to have type σi, the argument type of the effect Fi, and k to have type τi –[ϕ]→ τ, i.e. to be a continuation expecting a value of type τi, the result type of Fi.
The typing above is that of a deep handler. For a shallow handler, the continuation k would have the type τi –[ψ]→ σ instead of τi –[ϕ]→ τ. In the shallow case, the continuation is not covered by the handler; therefore, its type and effect are those of the handled expression, σ ! ψ. In the deep case, the continuation is handled; therefore, its type and effect are those of the handler, τ ! ϕ.
Hillerström and Lindley (2016) have shown the soundness of this type and effect system using a preservation-and-progress argument.
13.8 Limitations and extensions of row polymorphism
Row polymorphism is well-suited to type and effect systems. It not only assigns precise types to generic higher-order functions such as internal iterators, but also supports Hindley-Milner type inference (Milner, 1978) — the kind of type inference based on unification that is found in Haskell, OCaml, SML, etc. However, Hindley-Milner type inference is incompatible with subtyping and requires all subsumptions to be expressed in terms of row variable instantiation. This has some theoretical and practical limitations, which we will discuss now.
Imprecisions in effect typing. Row polymorphism does not account for the direction in which effects propagate. This can result in imprecise
typings. Consider:
g = λf: int –[ϕ]→ int. λb: bool.
handle (if b then f 0 else perform E ())
with { val(x) -> ret x; E(_, _) -> f 1 }
Because the function f is called in the same conditional that performs the effect E, the latent effect ϕ of f must acknowledge the presence of E:
However, the application f 1 in the handler for E has effect ϕ, as does the entire handle…with expression. Consequently, it appears that the effect E can always escape the handler, even though this is not the case when f does not perform E.
We could give f a polymorphic type such as τ1 = ∀ ρ, int –[ρ]→ int or τ2 = ∀ θ, int –[E:θ;ϕ]→ int. In this case, the effect type for the handler would no longer mentions E as present, but the whole function g could only be applied to functions f that are pure (in the case of τ1) or functions that do not perform effect E (in the case of τ2). There is no valid type for g that specifies it has exactly the same effects as f, regardless of what they are.
Verbosity of effect types. Rows contain a lot of information. This makes them difficult to read, especially in typing error messages. They are even more difficult to write in source code. Hindley-Milner type inference can alleviate this burden by automatically inferring many effect types along with value types, so programmers do not have to write them down. However, types must still be written manually in data type definitions and module interfaces.
When displaying types, it is possible to omit effect types that do not change the overall meaning of the type. For example, ∀ ρ, σ –[ρ]→ τ where ρ does not occur in σ or in τ can be displayed as a pure function type σ → τ. Similarly, the row F: θ; ϕ where θ is universally quantified and occurs nowhere else can be displayed as ϕ.
When writing type declarations by hand, a plain function type arrow → can be read as a pure function type:
| f: σ → τ ≡ f: ∀ ρ, σ –[ρ]→ τ
|
If there are several plain arrows in the type, it is usually safe to make them share the same row variable ρ, as in:
f: (σ → bool) → (σ → τ) → σ list → τ list |
| | ≡ | f: ∀ ρ, (σ –[ρ]→ bool) –[ρ]→ (σ –[ρ]→ τ) –[ρ]→ σ list –[ρ]→ τ list
|
|
In rare cases, this interpretation could be too restrictive for the actual implementation of function f. For example, this could occur if the implementation never calls its σ → bool argument. In this case, more precise effect types can be written explicitly in the declaration.
Closing and reopening row types.
In the system of section 13.7, “open” row types, which are terminated by a row variable ρ that can be generalized, are more flexible than “closed” row types, which are terminated by the empty row ∅. However, closed row types are easier to understand and simpler to display.
Leijen (2017) observes that it is possible to convert between “open” and “closed” row types for the latent effects of functions. Closing a row that is terminated by a variable ρ can be done by first generalizing ρ, and then instantiating it with ∅:
|
Γ ⊢ e : –[F1: π1; …; Fn: πn; ρ]→ τ ! ϕ ρ∉ FV(σ,τ,π1,…,πn)
| (close) |
| |
| Γ ⊢ e : σ –[F1: π1; …; Fn: πn; ∅]→ τ ! ϕ | |
|
Conversely, we can add the following typing rule to reopen a closed row by replacing the final ∅ with a row variable ρ, or more generally an arbitrary row ψ:
|
Γ ⊢ e : σ –[F1: π1; …; Fn: πn; ∅]→ τ ! ϕ | (open) |
| |
| Γ ⊢ e : σ –[F1: π1; …; Fn: πn; ψ]→ τ ! ϕ | |
|
Leijen (2017) suggests using rule (close) when typing let bindings, to remove as many row variables as possible before type generalization, and rule (open) when using let-bound variables, to regain the flexibility of open rows.
13.9 Further reading
More abstract presentations of type and effect systems can be found in Henglein et al. (2005), from the perspective of type systems, and in Nielson et al. (1999), from the perspective of static analysis. Pottier and Rémy (2005) is a reference on type inference, and includes a section on row types.
The value restriction plays a crucial role in reconciling mutable state and control operators with parametric polymorphism. It can be made more flexible by combining it with ideas from subtype polymorphism, as in the relaxed value restriction of Garrigue (2004), which is used in OCaml. Earlier solutions to the polymorphic reference problem include type and effect systems that track reference allocation effects (Talpin and Jouvelot, 1994), but these systems are significantly more complex than the value restriction.
The Koka experimental language (https://koka-lang.github.io) uses a type and effect system with row polymorphism to statically control algebraic effects (Leijen, 2014, Leijen, 2017). It is arguably the most advanced and usable implementation of a type and effect system available today.
Wadler and Thiemann (2003) build a correspondence between simple effect systems and hierarchies of monads. The F* language (Swamy et al., 2016) uses such a hierarchy of monads for typing effects.