| Figure 10.1: The stack-based implementation of effect handlers used in OCaml (Sivaramakrishnan et al., 2021). |
This chapter describes effect handlers for user-defined effects, a control operator that combines delimited continuations with exceptions. Effect handlers were introduced as a programming language construct by Bauer and Pretnar (2015), building on an earlier theory of algebraic effects that is presented in chapter 12.
Catching errors using exceptions. As shown in chapter 9, exceptions are often used to report errors that prevent a function from returning a normal result. For example, here is a parse_int function written in OCaml that converts strings to integers and raises the Conversion_error exception if the string is not recognized as an integer:
The exception is declared using the type exn += … syntax, which means that the type exn of exceptions is extended with a new Conversion_error constructor. This declaration is equivalent to exception Conversion_error of string, the declaration used in chapter 9, but it emphasizes the extensible nature of the exn type and shows the type of the Conversion_error exception constructor.
We can use parse_int to convert a list of strings and compute their sum:
If the list lst contains a bad string, a Conversion_error exception is raised, aborting sum_stringlist. This exception is handled in safe_sum_stringlist by printing an error message and returning a default result.
Fixing errors using effects. Let’s revisit the example above using a user-defined effect instead of an exception.
The differences are minor: perform is used instead of raise to raise the effect, and the declaration of the effect extends the eff type instead of the exn type. Note, however, that the eff type is parameterized by a type, which is int in the case of the Conversion_error effect, and which denotes the return type of the effect. More significant differences appear in the way effects are handled:
The effect handler (the effect part of the match construct) receives not only the value Conversion_error s of the effect, but also a continuation k, which it can use to restart the computation at the point where the Conversion_error effect was performed. Here, the handler prints an error message and then restarts the continuation with the value 0. This causes parse_int to return 0, and sum_stringlist to move on to the next elements of lst. For example:
Capturing and transforming effects. Effect handlers have much freedom in how they react to effects. Consequently, the same effect-performing code can have very different behaviors when executed inside different handlers. This is illustrated in the following example, taken from Pretnar (2015). Consider an effect Print that is performed when we want to produce some output.
Without a handler, this code is useless: running abc() will stop on an uncaught Print effect. We need to run it inside a handler that gives an interpretation to the Print effect.
The following handler executes the computation f(), turning Print effects into actual output on the terminal:
Unsurprisingly, output abc prints abc to the terminal. But another handler can collect all the Print effects of f() into a string and return this string at the end:
Now, collect abc will return the string "abc". Note the change of types: although the computation f still has the type unit -> unit, the handler produces a string, by turning the () return value of f() into the empty string, and by collecting the string values produced by continue.
A handler can also choose to re-emit the Print effect after some processing. For example, the following handler reverses the order in which the Print effects are generated by the computation f.
Running collect (fun () -> reverse abc) returns the string "cba". Alternatively, we can add a sequence number to each output:
Again, note the type change: the handler is of type int -> unit, where the int parameter is the current line number; it is applied to the initial line number 1.
Deep handlers vs. shallow handlers. Effect handlers come in two flavors, “deep” and “shallow”. A deep handler remains active until the handled computation terminates normally. If it catches an effect and restarts the continuation with continue, it will handle future effects. In contrast, a shallow handler disappears as soon as the handled computation terminates normally or performs an effect; it will not handle effects performed by the restarted continuation.
The match…with effect construct of OCaml implements deep effect handlers; therefore, all the examples shown so far use deep handling. Shallow handling is available in OCaml as functions from the Effect.Shallow library. If the safe_sum_stringlist example above used a shallow handler instead of a deep handler,
would still correct the error on xxx and still return 3, but
would not correct the error on yyy because the shallow handler would no longer be active at that point, so it would stop on an unhandled Conversion_error effect.
Effect handlers can express much more than restartable exceptions: like the control operators in section 8.5, effect handlers capture delimited continuations that can be used as first-class values.
The continuations captured by a handler. Consider a handler for the effect F around an expression e:
When e (or one of the functions it calls) performs the effect F, the continuation that is captured and bound to k extends from the perform (F v) expression to the end of the evaluation of e. In other words, the handler acts as a delimiter for that continuation.
When the continuation is applied to the value w, using continue k w, the evaluation of e restarts as if perform (F v) had returned the value w. In the examples seen so far, the continuation k is applied inside the handler h. However, this continuation is a first-class value: the handler h can also return it as part of its result, or store it in a data structure. (See the examples in sections 10.3 and 10.4.)
Typing the continuations. In OCaml, the type of the continuation k in the example above is (α, β) continuation, where α is the type of the values it expects and β is the type of the results it produces. The type α is determined by the type α eff of the effect F. The type β is the same as the type of the handled expression e. In summary:
|
Linear continuations in OCaml. The OCaml implementation of effect handlers has one limitation: continuations must be used linearly, that is, exactly once. In other words, the continuation k captured by an effect handler can only be restarted once, using continue k v. A special exception is raised the second time continue is applied to k. Moreover, if the continuation k does not need to be restarted, it should be explicitly discarded, using discontinue k e where e is an exception value, so that its resources are properly finalized.
This linearity condition is not part of the concept of effect handlers: other implementations, such as Eff and Koka, support full continuations that can be applied multiple times. However, OCaml’s linear continuations are compatible with a number of optimizations that the OCaml compiler performs and that become invalid when a continuation can be executed multiple times. In addition, they can be implemented efficiently by switching between multiple stacks, avoiding the cost of copying parts of the call stack. Consider again a handler for an effect F around an expression e:
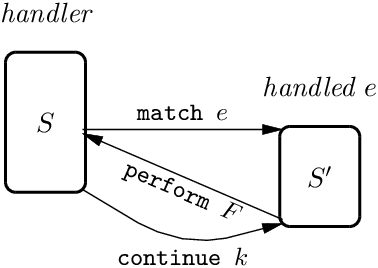
As depicted in figure 10.1, the handler executes on the initial stack S. It creates a new stack S′ to execute the handled expression e. When e performs the effect F, control is passed back to the handler h running on the stack S. The delimited continuation k is represented by the stack S′ itself. When k is restarted with continue k v, we switch back to the stack S′ and resume the execution of e. Execution keeps alternating between the stacks S′ and S until the handled expression e terminates normally or the continuation k is discarded with discontinue, at which time the auxiliary stack S′ is freed. Since k is used linearly, the stack S′ can be modified in place and does not need to be copied to protect against future modifications.
Figure 10.1: The stack-based implementation of effect handlers used in OCaml (Sivaramakrishnan et al., 2021).
Effect handlers make it easy to invert control in internal iterators and other higher-order functions, turning them into external iterators and generators.
From an internal iterator to a functional, external iterator. Continuing the examples from section 7.2, consider again a type of binary trees and an internal iterator over trees, which applies the given function to each value in the tree:
Here is an internal iterator (in the terminology of section 4.1) over trees:
We want to derive a purely functional external iterator tree_enumerator that returns the elements of the tree one by one. Here is the expected type:
We just need to perform an effect, called Next below, for each element of the tree. Then, the handler for Next will build the expected enumeration.
We use a local module named M to generate a fresh Next effect that remains local to each invocation of tree_enumerator and that matches the type elt of tree elements. Then, we use tree_iter to perform the effect Next x for each element x of the tree t.
The handler has two cases. If tree_iter returns normally, the traversal of the tree is over, there are no more tree elements to return, and we return Done. If tree_iter performs the Next x effect, we return a More constructor carrying the value x and the function obtained by the partial application continue k. When this function is applied, the tree_iter traversal restarts where it left off, producing more tree elements and eventually stopping.
The logic of this code is the same as that of the tree_enumerator example in section 7.2. However, in that example the internal iterator tree_iter is written in CPS, so that the function being iterated has access to its continuation as one of its parameters. Here, tree_iter is written in direct style, and the continuations are captured using an effect handler.
From an internal iterator to an imperative generator. As an alternative to the purely functional enumeration produced by tree_enumerator, we can also generate the elements of a tree one by one using internal mutable state, in the style of a Python generator:
The internal reference next holds a function of type unit -> elt. Each time this function is called, it returns the next element of the tree and updates next to continue traversing of the tree. Initially, the next function sets up a handler around tree_iter (fun x -> perform (Next x)) t. This handler catches the Next effect, updates next so that it will restart the traversal of the tree, and returns the current tree element. When all elements of the tree have been returned, the StopIteration exception is raised.
General control inversion. The approaches described above are not specific to tree traversals, nor to internal iterators: they can be used to turn arbitrary computations into Python-style imperative generators or into functional enumerators. The computation in question takes a function yield as a parameter, which it uses to send values to the outside world. For example, here is a function that sends all numbers in the [−n, n] interval:
We can test it by giving it a function that displays its argument:
We can also turn it into a Python-style generator by using the following generic function:
We can also generate a functional enumeration:
User-defined effects and effect handlers make it easy to implement cooperative multithreading as a library: many synchronization and communication mechanisms are easy to implement in terms of effects, and performance is quite good, especially with OCaml’s linear continuations and their implementation via stack switching.
Spawning and yielding. As in sections 7.3 and 8.3, we introduce multithreading with three functions: spawn f, to start the computation f() in a new thread; yield, to suspend the calling thread and restart another thread; and terminate, to abort the current thread. Since we have not yet decided on a scheduling algorithm, we implement the three functions as raising effects:
The actual behavior of these functions is determined by run f, an effect handler that surrounds the multithreaded computation f(), handles the Spawn, Yield and Terminate effects and schedules the threads. It uses a queue of ready threads represented as unit -> unit functions.
If the currently-executing thread terminates or performs the Terminate effect, we restart the first ready thread found in the runnable queue. If there are none, it means that the last running thread is exiting, so the whole multithreaded computation terminates.
If the currently executing thread performs the Yield effect to suspend its execution, we enqueue continue k, i.e. the unit -> unit function that restarts the current thread just after the yield point, as a ready thread, then restart another ready thread — or the thread that just suspended itself, if there is no other ready thread.
Finally, if the Spawn f effect is performed to request the creation of a new thread, the scheduler suspends the currently executing thread and gives control to f. It is necessary to use run f instead of just f() so that the effects performed during the execution of f() are handled properly.
We could have chosen a different scheduling strategy, where f is saved for future execution and the current thread continues to execute:
This simple scheduler is already sufficient to interleave the executions of several threads written in direct style:
This code prints A1 B1 A2 C1 B2 A3 C2 B3 A4 C3 A5 C4 C5 C6.
Communication channels. We now add support for communication channels, which allow threads to synchronize their executions while exchanging values. We provide a type α channel of communication channels that carry values of type α, a function new_channel to create channels, and two functions send and recv to send a value to a channel or receive a value from a channel. We implement “rendez-vous” communication in the style of the π-calculus: send on a channel blocks until another thread calls recv on the same channel; then, a value is communicated and both threads can restart.
Each channel consists of two queues, one for threads blocked on a send operation, one for threads blocked on a recv operation. At any given time, at least one of these queues is empty.
The send and recv operations are turned into effects, because they must be handled by the scheduler.
To handle the Send and Recv effects, we add two cases to the scheduler:
If the current thread sends the value v on the channel ch, and if there is at least one thread waiting to receive from this channel, this thread rc is removed from the receivers queue and restarted with the value v. However, if there are no threads waiting to receive from the channel ch, we add the current thread to the senders queue of ch and restart another thread.
Receiving a value from a channel ch is similar: if there is at least one thread sn waiting to send a value v, the thread sn becomes ready and we return v to the current thread; if there are no senders, we suspend the current thread, add it to the receivers queue, and restart another thread.
The scheduler above gives priority to receivers over senders. (Compare the two Some cases.) Different scheduling decisions can be easily implemented.
Promises. Another inter-thread communication mechanism is promises, also called futures. A promise is a value that is being computed and then made available to all threads. We represent a promise by its current value (initially None) and the list of threads waiting to receive this value:
There are two operations on promises: await, to block until the value of the premise is available and then return that value, and notify, to set the value of the promise. As usual, we represent these operations by effects:
One of the uses of promises is to compute values asynchronously, in a new thread. The result of the computation is made available via a promise.
As usual, we add cases to the run handler in order to implement the two operations over promises:
An Await effect either returns the value of the promise, if it is already determined, or adds the calling thread to the list of waiters for that promise and restarts another thread. A Notify effect sets the value of the promise and restarts all waiting threads with that value.
Overlapping I/O. A compelling use of cooperative threads implemented with effect handlers is overlapping input/output operations: threads can initiate I/O operations and suspend until the operation is complete. This way, only one thread is running at any time, but many I/O operations are going on at the same time. A textbook implementation of this approach is described in Dolan et al. (2017). The Eio OCaml library (https://github.com/ocaml-multicore/eio) provides an industrial-strength implementation of this approach.
We now give an operational semantics for effect handlers. Consider the following extension of the FUN language:
| Expressions: e | ::= | c ∣ x ∣ λ x . e ∣ e1 e2 | ||||
| ∣ | perform e | perform the effect e | ||||
| ∣ | handle e with eret, eeff | handle effects in e |
The expression perform e interrupts the current evaluation and branches to the next enclosing handle.
The expression handle e with eret, eeff evaluates the body e. If e evaluates to value v without performing an effect, the eret case is applied to v. If e performs the effect f, the other case, eeff, is applied to (f, k), where f is the value of the effect and k is the continuation of the perform, delimited by the handle.
The reduction semantics for effect handlers is close to that for delimited continuations (section 8.6) and that for exceptions (section 9.2). In addition to full reduction contexts C, we use handler-free contexts D to help us delimit the continuations:
| Reduction contexts: C | ::= | [ ] ∣ C e ∣ v C ∣ perform C ∣ handle C with eret, eeff | |||
| Handler-free contexts: D | ::= | [ ] ∣ D e ∣ v D ∣ perform D |
We then have the following two head-reduction rules for handle:
|
Notice how the subcontext D becomes the delimited continuation λ x . D[x] that is passed to the effect handler eeff along with the effect value v.
The second rule above describes the “shallow” kind of effect handling, where the handler disappears after handling an effect. The “deep” kind of effect handling is achieved by reinstalling the handler around the continuation D:
|
It is interesting to compare the reduction rule for shallow handlers with the rules for exception handlers (section 8.6) and those for delimited continuations (of the control0 kind, see section 9.2):
|
We see that exception handlers are effect handlers that do not capture the context D as a continuation. Control operators for delimited continuations capture the same continuations as effect handlers. However, the expression that receives this continuation comes from different places in the program: from the handler in the case of effect handlers, but from the capture in the case of delimited continuations. This minor difference in the formal semantics results in a significant difference in programming style and convenience: often, it is more natural and flexible to decide what to do with an effect at the place where the effect is handled rather than at the place where it is performed.
Hillerström et al. (2020) define a CPS transformation for effect handlers as an extension of the CPS transformation for delimited control operators described in section 8.8. In the case of delimited control, the transform 𝒞(e) of an expression e that is nested within n delimiters takes n+1 delimited continuations k0, …, kn as arguments. To support effect handlers, Hillerström et al. (2020) combine this approach with the double-barreled CPS of section 9.3: each delimited continuation ki is split into two continuations, ki for values that are returned normally and hi for effects that are performed. Consequently, the CPS transformation 𝒞(e) of an expression that is nested within n effect handlers should be applied to 2n + 2 continuations:
| 𝒞(e) k0 h0 k1 h1 … kn hn |
where the ki are the normal continuations and the hi are the effect handling continuations.
For the core FUN language, the CPS transformation is the familiar call-by-value transformation of section 6.5:
|
Note that the transformed terms operate only on the first value continuation (the one written k0 above). When 𝒞(e) is fully applied to 2n+2 continuations, the remaining 2n+1 continuations are unaffected by the transformation of core FUN constructs. For example, here is the fully applied translation of a constant c:
|
We see that the first normal continuation k0 is applied to the value c of the expression and to the rest of the continuation stack.
Here is the CPS transformation for performing effects:
| 𝒞(perform e) = 𝒞(e) (λ f. λ k. λ h. h (f, λ x. k x h)) |
The transformed code first evaluates e to a value f, which is the value of the effect. It then pops the first value continuation k and the first effect continuation h off the continuation stack, and applies h to the pair (f, λ x. k x h). Here, λ x . k x h is the partial continuation k wrapped as a function, ready to be used by the effect handler. When this function is applied, k receives h as its first continuation. This implements deep effect handling: the current effect handler h remains in place when the continuation is restarted.
For example, consider perform f where f is a constant:
|
Later, the continuation function λ x . k0 x h0 can be restarted with value v, in a different continuation stack k′0 h′0 … k′m h′m:
|
The continuation k0 is invoked as if perform f returned v, with the original effect handler h0 (because of deep effect handling) followed by the new continuation stack.
Finally, here is the CPS transformation for an effect handler:
| 𝒞(handle e with eret, eeff) = 𝒞(e) (λ v . λ h . 𝒞(eret) v) 𝒞(eeff) |
The effect handler evaluates 𝒞(e) after adding two continuations to the continuation stack: a value continuation λ v . λ h . 𝒞(eret) v, which pops h (the new handler continuation) off the stack and evaluates eret, and an effect continuation, which is just the transformation of the handler expression eeff.
In the case where e reduces to a constant c without performing an effect, we have the following evaluation:
|
In the case where e performs an effect, the perform applies the effect continuation, i.e. 𝒞(eeff), to a pair (vf, kf) of an effect value and a continuation value, resulting in the evaluation of
| 𝒞(eeff) (vf, kf) k0 h0 … kn hn |
which is just the application of eeff to (vf, kf).
The tutorial by Pretnar (2015) is a nice introduction to programming with effect handlers. Dolan et al. (2017) and Hillerström (2021, chapter 2) illustrate the use of effect handlers to write schedulers and operating system services, extending the multithreading example of section 10.4.
Effect handlers are currently supported by one mainstream language, OCaml (https://ocaml.org) and three experimental languages, Eff (https://www.eff-lang.org/), Effekt (https://effekt-lang.org/), and Koka (https://koka-lang.github.io). Some forms of effect handling are also provided as libraries for Haskell, JavaScript, and other languages. Sivaramakrishnan et al. (2021) describe the design and implementation of effect handlers in OCaml. The Koka design and implementation are described in Leijen (2014), Leijen (2017), Xie and Leijen (2021).