The theory of monads, as described in chapter 11, provides a generic account of the propagation and sequencing of effects. However, it says nothing about how effects are generated and implemented. Rather, each monad provides its own specific operations and their implementation.
The theory of algebraic effects, which is studied in this chapter, extends the theory of monads by providing a generic account of the generation and the handling of effects, independent of the specifics of a given monad. This theory inspired and provides the formal foundation for effect handlers, the control operator described in chapter 10.
A monadic language. As a running example in this section, consider the computational lambda-calculus of section 11.2 equipped with the operations get and set of the state monad and the operations choose and fail of the nondeterminism monad.
| Values: v | ::= | c ∣ x ∣ λ x . M | ||||
| Computations: M, N | ::= | v1 v2 ∣ if v then M else N | ||||
| ∣ | val v ∣ do x ⇐ M in N | |||||
| ∣ | get ℓ ∣ set ℓ v | mutable state | ||||
| ∣ | choose M N ∣ fail | nondeterminism |
At this point, we have not chosen a semantics for the combination of the state and nondeterminism monads: maybe we will backtrack the state on failure, but maybe we will persist the state and thread it through choice points. Can we still evaluate the do bindings, function calls, and conditional constructs of our language, while leaving the effectful operations uninterpreted?
Intermediate results. To answer the question above in the affirmative, we define a type R X of intermediate results. It describes all possible sequences of get, set, choose and fail operations that eventually return a value of type X.
|
This type has one constructor per operation, plus the Pure constructor for trivial computations that immediately return a value of type X. Each constructor has as many arguments of type R X as there are ways to continue the program: two ways for choose M N (the M way and the N way); zero ways for fail (execution is aborted); one way for set; and as many ways to continue get as there are values in the location being read, which we represent by a function Val → R X.
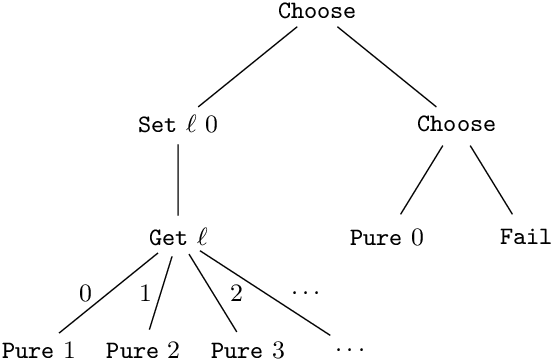
Trees of possible effects. Intermediate results can be thought of as a tree-shaped representation of all the effects that a program can perform. For example, consider the following program:
|
Its intermediate result is the following tree, with nodes containing constructors of the type R:

Since we are not interpreting the set and get operations, we do not know that, after set ℓ 0, get ℓ can only return 0. Instead, we consider all possible values x of get ℓ as subtrees of the Get node, and specialize the val (x+1) for each such value of x.
The monad of intermediate results. The type T X of intermediate results is a monad, with ret and bind defined as follows.
|
In other words, bind R f replaces every leaf Pure x in the tree R with f x. It is easy to check that the three monadic laws hold.
A denotational semantics. Using intermediate results, we can give our monadic language a denotational semantics. The denotation ⟦ M ⟧ of a monadic computation M of type T X is an intermediate result of type R X.
|
where the denotation v* of a value v is defined as
| c* = c x* = x (λ x . M)* = λ x . ⟦ M ⟧ |
Interpreting effectful operations. The denotational semantics ⟦ M ⟧ is independent of the semantics of the get, set, choose and fail operations. This semantics can be defined a posteriori as a “fold” traversal of the intermediate result, written run below.
If we choose to backtrack the store at choice points, run has type R X → Store → 𝒫(X) and is defined as
|
However, we can also choose to have a single store that is preserved across choice points. In this case, run has type R A → Store → 𝒫(A) × Store, and we take
|
The free monad. The type R X of intermediate results used in section 12.1 is an instance of a more general construction in category theory: the free monad. It can be described as the following type R X.
|
We have only one constructor Op, which takes a single argument of type F (R X) to describe all the operations of interest. The type constructor F: Type → Type is a functor: it comes with a functorial map operation
| fmap: ∀ A, B, (A → B) → (F A → F B) |
that lifts any function A → B to a function F A → F B.
We can recover the type R used in section 12.1 by taking
|
The corresponding fmap operation is, not surprisingly,
|
The presentation of the free monad in terms of a functor F makes it possible to define ret and bind operations generically, with the help of fmap.
|
The freer monad. The freer monad by Kiselyov and Ishii (2015) is another generic construction of a type of intermediate execution results for monadic programs.
|
Here, Eff B is the type of effects that produce a result of type B. Each effect corresponds to a constructor of type Eff. Adding new effects means extending the type Eff with new constructors, as in the OCaml presentation of user-defined effects (chapter 10).
If ϕ has type Eff B, the subtrees of Op ϕ k are k b for each b : B. There are as many subtrees as there are elements in B. The k argument acts as the continuation for the effect ϕ, receiving the return value of the effect as its argument and producing the subtree that describes the rest of the execution.
For example, here are the effect constructors for mutable state and for nondeterminism:
|
We can encode the choose operation using the Flip effect:
| choose R1 R2 ≜ Op Flip (λ b . if b then R1 else R2) |
The presentation of the freer monad in terms of the Eff type constructor also makes it possible to define ret and bind generically:
|
Note that we no longer need a functor and its fmap operation to define bind.
Interpreting effectful operations in the freer monad. We can interpret the effects described by a term of the freer monad by using the following generic “fold” over that type:
|
The fold interpretation takes two functions as arguments, f to handle pure computations and g to handle effects.
For mutable state and nondeterminism, the interpretation where the state is backtracked at choice points is obtained by taking
|
The other interpretation, where the state is preserved at choice points, is left as an exercise.
Note the control inversion present in the definition of fold: syntactically, it looks like the program calls the operations (get, set, etc.) of the monad; operationally, it’s the implementation of these operations (the function g) that evaluates the program on demand, using the continuation k to restart its evaluation.
Interaction trees. Interaction trees (Xia et al., 2020) are a coinductive version of the type R X of the freer monad. Interaction trees can have infinite branches, which makes them capable of describing divergence (computations that do not terminate). They are obtained by interpreting the following type definition coinductively, i.e. as a greatest fixed point instead of the least fixed point used for inductive definitions.
|
The constructor Tau denotes one step of computation that performs no effect. Silent divergence (e.g. an infinite loop) is represented by an infinite sequence of Tau steps:
| ⊥ = Tau ⊥ that is, ⊥ = Tau (Tau (Tau (⋯))) |
Infinite interaction trees can also contain infinitely many effects. Consider the nondeterministic program
| let rec f () = if flip () then 0 else f () |
Its interaction tree is
| X = Op Flip (λ b . if b then Pure 0 else Tau X) |
with an infinite branch corresponding to the case where flip always returns false.
The Tau representation of silent computation steps is necessary to capture silent divergence, but causes programs that differ only in the number of silent steps performed to have different interaction trees. This is generally undesirable. Therefore, interaction trees are considered equal up to weak bisimilarity, i.e. the removal of finite sequences of Tau steps. Writing ≈ for weak bisimilarity,
| Pure v ≈ Tau(Pure v) ≈ Tau(Tau(Pure v)) ≈ ⋯ |
However, Pure v ≉⊥ since ⊥ is an infinite sequence of Tau steps.
In the following, we will use “interaction tree” to mean either “term of the freer monad” (inductively defined) or “interaction tree a la Xia et al. (2020)” (coinductively defined).
We now recall some notions from algebra that help to understand why free monads are free and why algebraic effects are algebraic. Bauer (2018) gives a more detailed account.
Algebraic structures. An algebraic structure (like a group, a ring, a monoid, etc.) is described by
For example, a monoid (or semigroup) is (T, ε, ·) where
|
and the following three equations hold:
|
Likewise, a group is (T, 0, +, −) where
|
Theories vs. models. When discussing algebraic structures, it is useful to keep in mind the distinction between theories and their models. A theory is just the signature of the operators (names and types) and the equations they must satisfy. A model of a theory is a definition of the support and of the operations that satisfy the equations.
For example, the theory of monoids is
|
The following structures “are monoids”: more precisely, they are models of the theory of monoids.
|
The free monoid. Given a set (an “alphabet”) A, the free monoid over A is (A*, ε, ·) where
If A = {1,2,3}, for example, “12”, “333” and “2” are words, and we have
| 12 · (333 · 2) = (12 · 333) · 2 = 123332 |
There are other monoids whose carriers include A, such as (ℕ, 0, +) in the example above. However, the free monoid over A is “the simplest”, or “the least constrained”, of all monoids whose carriers contain A. This intuition can be made mathematically precise: for any monoid (B, 0, +) with A ⊆ B, there exists a morphism Φ that injects the free monoid (A*, ε, ·) into (B, 0, +). The function Φ : A* → B is defined as
| Φ(ε) = 0 Φ (a1 a2 … an) = a1 + a2 + ⋯ + an |
This is the “fold” of the operation + over the list a1 a2 … an, with 0 as starting value. The function Φ is a monoid morphism, since it commutes with the two monoid operations: Φ(ε) = 0 by definition, and Φ(w1 · w2) = Φ(w1) + Φ(w2) by associativity of +.
Free models. The free monoid and its characterization in terms of monoid morphisms is a special case of the general notion of free models for algebraic theories.
Consider a theory 𝒯 and a set X of elements of interest. A free model of 𝒯 generated by X is a 𝒯-model M and a function η : X → carrier(M) such that:
For every other 𝒯-model M′ and function η′ : X → carrier(M′), there exists a unique morphism Φ : M → M′ such that η′ = Φ ∘ η.
In the previous example with the free monoid generated by A, the other monoid is (B, 0, +) with A ⊆ B, η is the trivial injection A → A*, and η′ is the trivial injection A → B.
It is instructive to construct free models for familiar algebraic structures. For example, the free group generated by the set X is the set of linear combinations c1 x1 + ⋯ + cn xn of elements xi ∈ X with integer coefficients ci ∈ ℤ, or, in other words, the type X → ℤ of functions c mapping x to its coefficient c(x), equipped with pointwise operations.
|
An algebraic theory of monads. We can define a theory of monads in the style of the algebraic theories in section 12.3. The operations are ret, bind, and F for each effect F specific to the monad (e.g. the get and set for the state monad). Here is the signature for these operations:
|
In the F case, A is the type of the argument of the effect F and B the type of its result. Thus, the F operation takes as argument the argument of the effect (of type A) and a continuation (of type B → T X) that receives the result of the effect.
The signature above stretches the notion of algebraic theory a bit: the carrier is a parameterized type T X instead of a simple type, and the operations take functions as arguments. Nevertheless, the basic notions from section 12.3 remain applicable, especially the notion of morphism between structures.
The equations of the theory of monads are the three monadic laws, plus a commutation law between F and bind. (More equations can be added to characterize particular effects; see section 12.5.)
|
Free monads are free. It is easy to see that the free monad and the freer monad from section 12.2 are models of this theory of monads. In the following, we will concentrate on the freer monad. The carrier T is the following inductive type of interaction trees:
|
The specific operations F are the constructors of the Eff type. The ret, bind and F operations are defined by
|
The four equations of the theory follow easily from the definition of bind. Therefore, the freer monad is a model of the theory of monads.
We now show that the freer monad is a free model generated by the set F of effects of interest. Consider another model M = (T′, ret′, bind′, F′) for the same set of effects F. We define a morphism Φ from the freer monad to M by
|
This morphism commutes with the monad operations. For ret and for F, this follows immediately from the definitions:
|
For bind, we proceed by induction and case analysis on the interaction tree:
|
Building on the algebraic presentation of monads, we now define a small language that accounts not just for the propagation of effects, like Moggi’s computational lambda-calculus, but also for the generation of effects.
The language extends the computational lambda-calculus with one construct to perform an effect.
| Values: v | ::= | x ∣ c ∣ λ x. M | |||||
| Computations: M, N | ::= | v v′ | application | ||||
| ∣ | if v then M else N | conditional | |||||
| ∣ | val v | trivial computation | |||||
| ∣ | do x ⇐ M in N | sequencing | |||||
| ∣ | F(v; y . M) | performing an effect |
The computation F(v; y . M) performs effect F with arguments v (zero, one or more values). The effect produces a result value that is bound to y in the continuation M.
We write F(v ) for F(v; y . val(y)), that is, the effect F with the trivial continuation that immediately returns the value of the effect.
Generic laws. Following the same approach as in section 11.2, we equip our language of algebraic effects with an equational theory to show that two computations are equivalent. This theory contains the following generic laws:
|
The first six laws are those of the computational lambda calculus, with laws (M1), (M2) and (M3) reflecting the familiar three laws of monads. The last law, (M4), comes from the algebraic presentation of monads (section 12.4) and equates two ways of performing an effect F and then binding its result. In particular, (M4) and (M1) imply
| F(v; y . M) ≡ do y ⇐ F(v ) in M |
For some families of effects, the laws above are complete: no other equivalences between effectful computations hold. This is the case for input/output effects (print and read effects), which never commute or cancel. The profound insight of Plotkin and Power (2003) is that other effects such as mutable state or nondeterminism can be characterized by adding specific laws to the equational theory.
Laws for mutable state. The get and set effects that implement mutable state have a rich equational theory. First, after a location ℓ is set to a value v, ℓ contains v and every other location ℓ′ ≠ ℓ is unchanged. These so-called “good variable properties” are captured by the following two laws:
|
These two laws are sufficient to execute stateful programs and determine their final values. For example, assuming ℓ′ ≠ ℓ,
|
To obtain a complete characterization of mutable state, we must add the following laws:
|
Laws for nondeterminism. The operations fail and choose of the nondeterminism monad also enjoy a rich equational theory. First, fail is absorbing, since it returns no value and thus ignores its continuation:
| fail( ; y . M) = fail( ) for all M |
Second, fail is the identity for choose:
| choose M fail( ) = choose fail( ) M = M (identity) |
Third, choose is idempotent, commutative, and associative:
|
In our language, choose M N is encoded as flip(, y . if y then M else N), where flip is the effect that nondeterministically returns true or false. Therefore, the laws above should be read as laws for flip; but then they become much harder to read.
The laws above are those of a semilattice, with choose acting as the join operation and fail as the identity element. They correspond to using sets of results to implement the nondeterminism monad. When lists of results are used instead, as in Haskell’s List monad, the order and multiplicity of the results matter. Therefore, the “idempotent” and “commutative” laws must be removed. The remaining laws, then, are those of a monoid, with choose as the composition operator and fail as the identity element.
Denotational semantics. To each computation M, we associate an interaction tree ⟦ M ⟧:
|
If we want to support general recursion and partiality, we need to use coinductive interaction trees and add Tau steps in places that can cause divergence, such as function applications. Otherwise, inductive interaction trees will suffice.
To obtain the result of the execution of the computation M, we interpret the tree ⟦ M ⟧ in an appropriate monad, using the “fold” operation over trees from section 12.2:
| run M ≜ fold f g ⟦ M ⟧ |
where f and g provide interpretations for the constructors Pure and Op of interaction trees.
It is easy to check that the laws of the equational theory are satisfied by this semantics: if M ≡ N, then run M = run N. For the seven generic laws, we have a stronger result: if M ≡ N, then ⟦ M ⟧ = ⟦ N ⟧. This follows from the definition of ⟦ · ⟧ and of bind on interaction trees.
For laws specific to some effects, the verification also involves the definitions of fold and of the f and g interpretation functions. For example, in the case of nondeterminism, we define
|
Then, after simplifications, the laws for nondeterminism shown above follow from basic properties of set union:
|
Similarly, the laws for mutable store follow from standard properties of store updates in a store-passing implementation.
In sections 12.2 and 12.5, interaction trees ⟦ M ⟧ representing the effects performed by a computation M are interpreted in the monad of our choice by “folding” the interpretation functions f and g over the tree:
|
So far, we have chosen to perform a single “fold” to handle all the effects at once and directly produce the final meaning of the program. However, such a “fold” can also produce a simplified interaction tree as a result. Let us call such a transformation of interaction trees into interaction trees a semantic effect handler, or just effect handler for short.
Effect handlers can be composed. This makes it possible for a handler to handle only a subset of the effects, while leaving the other effects unchanged in its result. A handler can also choose to implement an effect by translating it to other effects. In both cases, it expects to be composed with another handler that can interpret the remaining effects.
For example, here is a handler for the get and set effects that implement mutable state:
|
This handler adds a store σ as a parameter, which it uses to interpret get as a store access and set as a store update. Consequently, the resulting interaction tree does not contain any get or set effect. All other effects ϕ are re-emitted in the resulting interaction trees and leave the store unchanged.
As another example, here is a handler for the fail and flip effects that implement nondeterminism:
|
There are two different ways to compose the state and nondet handlers:
| run1 t σ = nondet (store t σ) run2 t σ = store (nondet t) σ |
Given a tree t of type R A, both compositions return a tree of type R (𝒫(A)). Moreover, if t contains no effects other than get, set, fail and flip, both compositions return a trivial tree Pure s, where all effects have been handled, producing the final set s of results. However, the two compositions implement two different semantics of state in the presence of nondeterminism: run1 backtracks the store when fail causes flip to be re-executed, while run2 threads a single store throughout execution.
The second profound insight that led to the discovery of effect handlers as control operators is that of Plotkin and Pretnar (2013), who not only introduced the idea of effect handlers as transformers of interaction trees, but also showed that these effect handlers can be defined within programs, using a small extension of the language of algebraic effects in section 12.5.
Syntax of handlers. The extended language has the following syntax:
| Values: v | ::= | x ∣ c ∣ λ x. M | |||||
| Computations: M, N | ::= | v v′ | |||||
| ∣ | if v then M else N | ||||||
| ∣ | val v | ||||||
| ∣ | do x ⇐ M in N | ||||||
| ∣ | F(v; y . M) | ||||||
| ∣ | with H handle M | (effect handler) | |||||
| Handlers: H | ::= | { val(x) → Mval; | |||||
| F1(x; k) → M1; | |||||||
| ⋮ | |||||||
| Fn(x; k) → Mn } |
The new language construct with H handle M handles some of the effects performed by the computation M as described by the handler H. Table 12.1 shows the informal semantics of this construct, depending on whether M terminates normally, or by performing one of the effects Fi, or by performing another effect, and whether we use “shallow” or “deep” semantics for effect handling.
Behavior of M Shallow handling Deep handling
x = v
x = v
x = v and
k = λ y . N
x = v and
k = λ y . with H handle N
Table 12.1: Behavior of with H handle M, where H = { val(x) → Mval ; …; Fi(x; k) → Mi ; … } .
Denotational semantics of effect handlers. The denotation ⟦ H ⟧ of an effect handler is a transformer of interaction trees, so that the denotational semantics of the with construct is just an application of this transformer:
| ⟦ with H handle M ⟧ = ⟦ H ⟧ ⟦ M ⟧ |
This transformer is a “fold” traversal of the tree, in the case of deep handling, and a “case” analysis at the top of the tree, in the case of shallow handling:
| ⟦ H ⟧ = |
|
The difference between a “fold” and a “case” is apparent in both their definitions and their types:
|
For a handler H = { val(x) → Mval ; F1(x; k) → M1; …; Fn(x; k) → Mn }, the semantics ⟦ H ⟧ret for normal termination and ⟦ H ⟧eff for termination on an unhandled effect are
|
The course notes of Bauer (2018) explain the algebraic nature of algebraic effects and handlers in more detail than I could give in this chapter.
As shown by Plotkin and Power (2008) and re-explained in section 4 of Bauer (2018), a coalgebraic interpretation of effects can be used to account for “hardware” or “real-world” effects such as I/O that are performed outside of the program and cannot be rolled back by the program. Then, the complete semantics for a computation is described as a tensor product between a model for the “software” effects and a comodel for the “hardware” effects.
The theory of algebraic effects is “first order” in nature, in that it does not consider effectful operations that take computations (not just values) as arguments. The choose M N operation of the nondeterminism monad can be accounted for by the encoding if flip then M else N. But the trywith operation of the exception monad cannot be represented as a first-order effect. Several theories have been proposed to account for these higher-order effects, such as the scoped effects of Yang et al. (2022).