Continuation-passing style (CPS) was introduced in chapter 6 as a semantic device, with CPS transformations making reduction strategies explicit in functional languages. In this chapter, we show that CPS and variants are also a useful programming technique in functional languages, giving functions access to the continuations of their calls. This makes it possible to implement a number of advanced control structures (generators, coroutines, backtracking, etc.) as library functions in any functional language.
The defining characteristic of CPS is that functions do not return their results normally; instead, they always pass their results to continuations given as additional arguments. For example, consider the naive factorial function written in OCaml in the standard direct style:
In continuation-passing style (CPS), this function takes an extra argument k, which is the continuation to call with the result of the computation:
Note the change in types: int → int for the direct style function, but ∀ α . int → (int → α) → α for the CPS function. Here, α is the type of the final result of the continuation. It is determined by the continuation passed to cps_fact.
The function cps_fact above can be produced mechanically, by applying one of the call-by-value CPS transformations from section 6.5 to the definition of fact. However, CPS transformations are designed to be applied to the whole program, while CPS programming often introduces continuations selectively: not for all functions, but only for those functions that benefit from CPS. For example, instead of converting all callers of cps_fact to CPS, some callers can remain in direct style, calling cps_fact n (fun r -> r) as the equivalent of fact n.
Why write functions in CPS? One reason is that recursive functions in CPS run in constant stack space: all recursive calls are tail calls. This does not mean that they run in constant space: the activation records that would be allocated on the stack in direct style are allocated (in the form of function closures) in the heap in CPS. Using heap space instead of stack space can still be advantageous in the case of language implementations that artificially limit the size of the stack.
But the main motivation for programming in CPS has nothing to do with these implementation considerations: it is to give CPS functions the ability to manipulate their continuations in ways other than just calling them with a final result.
Consider binary trees with values at the nodes:
Here is an internal iterator (in the terminology of section 4.1) over trees:
Let us rewrite it in CPS, adding continuation arguments to tree_iter and to the argument f:
As shown by its type above, the function f takes as argument not only an element x of the tree, but also a continuation that captures the traversal of the tree elements that come after x. If f is written in standard CPS, it will do something with x and then invoke k, as in
However, f can use k differently. For example, it can store k in a reference for later use, thus obtaining a Python-style generator (imperative external iterator) over trees:
When the generating function returned by tree_generator t is first called, tree_iter starts traversing the tree, calling fun x k -> ...
on the leftmost element x of the tree. This function stores the continuation of the traversal in reference next and then returns x to the caller. Subsequent calls to the generating function will restart the traversal where it left off, stopping at the next element in an in-order traversal and returning it.
We can also obtain a purely-functional external iterator from the tree_iter function, using lists computed on demand as the result:
Given a non-empty tree t, calling tree_enumerator t returns
More(x, k) where x is the leftmost element of t and k applied to () enumerates the following elements of t.
Computations written in CPS can suspend themselves at any point in the program, by storing the continuation in global data and relinquishing control entirely. An external agent such as a scheduler or a graphical user interface (GUI) can then restart the continuation when the time comes.
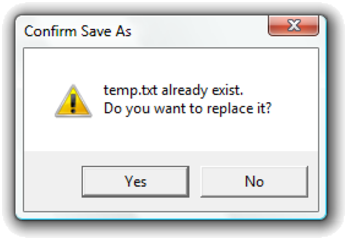
Consider a dialog box in a GUI application written in CPS:

The function dialog_box_yesno can attach the given continuation as callbacks to the “Yes” and “No” buttons, then return control to the main event loop. This way, the GUI remains responsive while the dialog box is displayed.
Generalizing this pattern, we can easily implement cooperative multithreading for CPS computations. Suspended threads are represented as unit -> unit continuations and stored in a global queue named ready. The schedule function restarts one of these suspended threads.
The threading library provides three operations: yield, to suspend the calling thread and restart another thread; terminate, to stop the execution of the calling thread, but keep other threads running; and spawn f to start the computation f() in a new thread.
Note that yield takes a continuation as an argument, forcing the caller to be written in CPS. For example, here is a process that prints integers from 1 to count, with the given prefix, yielding control after each print:
When run in isolation, process behaves sequentially: process "A" 5 prints A1 A2 A3 A4 A5. When several processes are run concurrently, they interleave execution at the yield points. For example,
prints C1 A1 B1 C2 A2 B2 C3 A3 B3 C4 A4 C5 A5 C6.
A function written in CPS can take several continuations instead of just one. Each continuation corresponds to a different way to exit the function, not unlike the multiple return points of Fortran 77 subroutines (see section 3.4). For example, here is a quadratic equation solver with two continuations, one for the case where there are real solutions and one for the other case:
We have also chosen to pass the two roots x1 and x2 as two arguments to the continuation k1 instead of as a pair (x1, x2), to show that we can return several results this way. A typical use of quadratic would then be:
This technique of using two continuations, one for the success case and one for the failure case, can be used to implement structured exceptions, via a variant of the CPS transformation known as the double-barreled CPS transformation; see section 9.3.
Like exceptions, Prolog-style backtracking can also be implemented using two continuations, one for success and one for failure, the latter triggering backtracking to the last choice point. The main difference with exceptions is that the success continuation takes the failure continuation as an argument, in addition to the returned value.
For example, consider regular expression matching. A regular expression parser is a function that takes a word w (a list of characters) and two continuations ksucc and kfail. If w can be decomposed as w = w1 . w2 with w1 matching the regular expression, then ksucc is applied to w2 (the rest of the input) and to kfail. Otherwise, kfail is called. This is reflected in the following OCaml types:
Here are parsers for single characters (char), for empty words (epsilon), and for the empty language (empty):
Here are parser combinators which, given parsers for regular expressions r and r′, construct parsers for concatenation (r . r′), alternation (r ∣ r′), and repetition (r*):
The repetition star r always succeeds: either by matching r then star r again, or by matching the empty string. However, when matching r, we must make sure that at least one character of the input was matched, hence the check List.length w’ < List.length w and the backtracking if this check fails.
The implementation of star r above follows a greedy strategy: it tries to match r as many times as possible, then goes back in case of failure. Here is an alternative implementation of star r that follows a non-greedy strategy, trying to match r as few times as possible.
To determine whether a word matches a regular expression, we call its parser with a failure continuation that returns false and a success continuation that returns true if all characters were matched, or backtracks otherwise:
As an example where backtracking is necessary, consider matching the word w = ab against (a ∣ a.b): the first alternative, a, produces a partial match, leaving b unmatched; backtracking is necessary to try the second alternative a.b, which matches w completely.
A function written in standard CPS never inspects the result of the continuation it takes as an argument: the function either calls the continuation in tail position, or wraps it in another continuation. This is reflected in the type of the function, which is often polymorphic in the return type of the continuation, as in the cps_fact example in section 7.1.
For some applications, it may be useful for a function to use the value returned by its continuation, as a kind of feedback from the continuation about the suitability of the result passed to the continuation. For example, the continuation can return a Boolean value, where true means “the result you gave me is correct” and false means “please give me another result”.
Here is the regular expression matching example above rewritten in this style. A parser now has a single continuation of type char list -> bool, which takes as argument the rest of the input word (the suffix that did not match) and returning true if this residual input is recognized and false otherwise. The parser itself returns true if the input word was fully matched, and false otherwise.
In the code of section 7.5, backtracking was triggered by invoking the fail continuation; here, it is triggered by returning false. The Boolean “or” (the || operator) is used to try another alternative if the first alternative fails.
Instead of returning Booleans that say whether a solution was found, continuations can return integers that count how many solutions exist. In this style, the base functions enumerate several possibilities, pass them to the continuation, and sum the returned counts.
For example, here is a function that enumerates Boolean values, and another that enumerates integers between lo and hi:
We can use the int generator to enumerate all the throws of three 6-sided dice and count how many throws result in 16 or more. (The answer is 10.)
For a more interesting example, we can enumerate all AVL balanced binary trees of height h, measuring them using the continuation k:
In an AVL tree, the heights of the two subtrees of a node must differ by at most one. Thus, if a tree has height h, its two subtrees have heights h−1, h−1 or h−1, h−2 or h−2, h−1. The helper function avltree2 generates nodes (non-empty trees) with value 0 and subtrees of respective heights hl and hr. By evaluating avltree 4 (fun _ -> 1), we learn that there are 315 AVL trees of height 4.
Finally, instead of returning integer solution counts, we can also return probabilities represented as floating-point numbers in the [0,1] range. Continuations k, then, play the role of measures for the different possibilities enumerated by the functions. For example, here are the enumerators for Booleans and for integers in the [lo,hi] range, using measures instead of counts:
Then, we can compute the probability of scoring exactly 15 on a three 6-sided dice as follows. (The answer is about 4.6%.)
Chapters 5 and 6 of Friedman and Wand (2008) show other examples of programming with continuations, in particular for writing interpreters for languages featuring exceptions or concurrency.
CPS can also be used as an intermediate representation in optimizing compilers for functional languages, as in the RABBIT (Steele, 1978) and SML/NJ (Appel, 1992) compilers. Kennedy (2007) discusses advanced compiler optimizations that are easy to perform on a CPS-based intermediate representation.