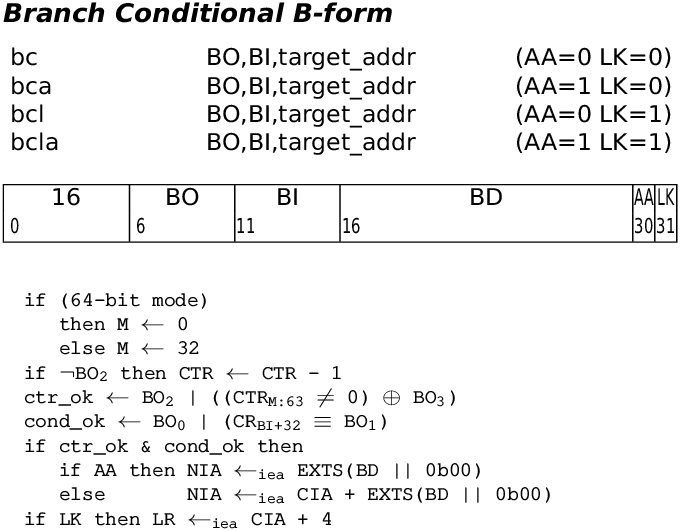
| Figure 1.1: The “branch conditional” instruction of the Power instruction set architecture. (Source: OpenPOWER Foundation, Power Instruction Set Architecture, version 3.1C, 2024.) |
Most computing devices today are programmable computers with stored program, meaning that the program that describes the computation is stored in memory along with the data on which it operates. This computer organization is known as “the von Neumann architecture”, because it was first described in a technical report by von Neumann (1945). A similar architecture is described by Turing (1946).
Program counter and branches. In a von Neumann architecture, the central processing unit (CPU) has a special register, the program counter (PC), which holds the address of the memory word containing the next instruction to be executed. Most instructions (arithmetic and logic operations, memory reads and writes, etc.) increment the PC when they are executed, making it point to the next instruction in memory. This ensures sequential execution of the instructions stored in memory. In contrast, branch instructions explicitly set the value of the PC, making it possible to jump to any point in the program.
For example, the following machine code for the x86 processor family produces the factorial numbers 1!, 2!, …, n!, … on output port 32. (The actual machine code is the hexadecimal numbers in column 2. A disassembly of the machine code is shown in column 3 to help understand it.)
0: b8 01 00 00 00 mov eax, 1 ; eax contains n! 5: ba 01 00 00 00 mov edx, 1 ; edx contains n 10: e7 40 out 32, eax 12: 83 c2 01 add edx, 1 15: 0f af c2 imul eax, edx 18: eb f6 jmp 10
The PC successively takes the values 0, 5, 10, 12, 15 and 18 as the first five instructions are executed in sequence. The jmp 10 instruction, encoded by the two bytes eb f6, sets the PC back to value 10, creating an infinite loop around the out, add and imul instructions.
Conditional branches. Modern processors offer conditional branch instructions that set the PC to a given value if some condition on the registers is true, but continue in sequence if the condition is false.
For example, here is a counted loop that, given n in register edx, computes n! and outputs it:
0: b8 01 00 00 00 mov eax, 1 5: 0f af c2 imul eax, edx 8: 83 ea 01 sub edx, 1 11: 75 f8 jnz 5 ; jump to 5 if not 0 13: e7 40 out 32, eax
The instruction written jnz branches if the previous result was not zero, and continues in sequence otherwise. It causes the imul/sub loop body to be executed n times, until register edx drops to zero. Execution then continues with the out instruction following the jnz.
Historical alternative: self-modifying code. Conditional branch instructions are not part of the original designs of von Neumann and Turing. Instead, both authors rely on the fact that the code is stored in memory, and can therefore be modified during program execution, by writing to the appropriate memory locations. This is called self-modifying code.
For example, here is how to jump 100 bytes forward when register edx is 1 and continue in sequence when register edx is 0, by synthesizing and then executing the appropriate jmp +100 or jmp +0 instruction.
0: 6b c2 64 imul eax, edx, 100
3: 88 05 01 00 00 00 mov 1(rip), al
9: eb ?? jmp ?? ; dynamically modified
The byte following the eb opcode is the relative address of the target of the branch. The mov instruction writes 0 (if edx is 0) or 100 (if edx is 1) in this byte. It then increments the PC and executes the jmp instruction at 9, which branches to PC 11 (if edx is 0) or 111 (if edx is 1).
Self-modifying code is difficult to set up and degrades the performance of pipelined processors. This is why, during the 1950s, conditional branch instructions and indexed memory addressing became standard in processor instruction sets, replacing the two most common uses of self-modifying code.

Figure 1.1: The “branch conditional” instruction of the Power instruction set architecture. (Source: OpenPOWER Foundation, Power Instruction Set Architecture, version 3.1C, 2024.)
Machine language is the programming language that can be executed directly in hardware by the CPU circuits. A machine language program consists of the bit-level encodings of the program’s instructions as they are stored in memory during execution. Each instruction set architecture (ISA) defines its own machine language. Many ISAs encode each instruction as a 32-bit word; some use variable-length encodings. The encodings are documented in the ISA reference manual. For example, figure 1.1 shows the encoding of the conditional branch instruction in the Power ISA. In the 32-bit word that encodes this instruction, some bits (the opcode) are fixed and identify the instruction. Other bits encode the condition for branching, the target of the branch, and possible side effects on the LR and CTR registers.
Assembly language is a textual representation of machine language, much easier for humans to write and read, but close enough to machine language that a simple program called an assembler can automatically translate from assembly language into executable machine code. The first assembler appeared in 1947 in Kathleen Booth’s work on the ARC computer.
Assembly language uses mnemonics to name processor instructions (like the mov, imul, jmp mnemonics used in the examples above), and labels to name program points and branch targets. It also supports comments to document the code. Comments are ignored by the assembler, but greatly help humans to understand and maintain the code.
Here is the computation of n! above, rewritten in x86 assembly language. Comments start with a semicolon character “;”.
; Compute factorial of n.
; n is passed in edx.
; n! is left in eax.
; edx is clobbered.
mov eax, 1 ; initialize eax to 1
again: imul eax, edx ; multiply eax by n
dec edx ; decrement n
jnz again ; repeat while n is not 0
; here, eax contains n!
Note the use of a symbolic label, named again, to denote the location of the imul instruction, making it easy to express jumps to that location, as in the conditional branch jnz again.
While much easier to work with than machine language, assembly language remains in one-to-one correspondence with the instruction set architecture: each opcode corresponds to one of the instructions supported by the processor; each line of source text produces one binary-encoded machine instruction.
Macro-assemblers, or autocoders as IBM called them, are sophisticated assemblers that support additional opcodes beyond those corresponding to the processor instructions, thus providing programmers with a richer assembly language. These extended opcodes, also called macro-instructions, are expanded into canned sequences of processor instructions during translation to machine code.
Macro-instructions are often used to write various types of loops concisely and clearly. For example, a counted loop, with register ecx ranging from 0 to 99, can be expressed by two macro-instructions, begin_loop and end_loop, expanded as shown at right:
; Source code ; Code after macro-expansion mov ecx, 0 begin_loop lbl, ecx, 0 lbl: ... ... ... ... end_loop lbl, ecx, 100 inc ecx cmp ecx, 100 jne lbl
begin_loop initializes the loop index register and associates a label with the first instruction of the loop body. end_loop increments the loop index and re-executes the loop body if it has not reached the final value of the index.
Flowcharts are an important tool for programming in assembly language. A program flowchart is a graphical representation of a program or program fragment, using boxes to represent basic computational steps and arrows to represent the flow of control. For example, here is a flowchart for a counted loop that prints five “star” characters:
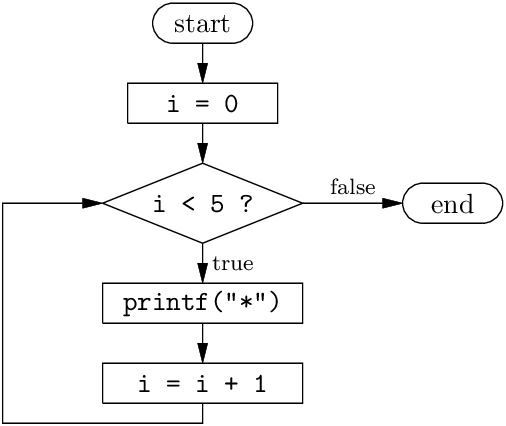
In the period from 1945 to 1985, from the first modern computers to the widespread adoption of structured programming, flowcharts were the preferred way to design and document programs. Flowcharts omit a number of details such as the exact sequences of instructions that implement the boxes, the order in which they occur in the code, and the labels and branches used to implement the flow of control. This is a strength of flowcharts: they present a higher-level, less cluttered view of the program than the assembly code. This is also a weakness: substantial manual work is required to translate a flowchart into assembly code, and it is difficult to keep the flowchart and the code in sync as the program changes.
Expressions. Fortran I, introduced by IBM in 1957, is the first programming language to supports general expressions written in algebraic notation. (Hence its name, which stands for “FORmula TRANslator”.) For example, the solutions X1 and X2 to the quadratic equation Ax2 + Bx + C = 0 are concisely expressed in Fortran:
It is the job of the Fortran compiler to implement these expressions using elementary processor instructions, using registers or temporary variables to hold intermediate results. For reference, here is the AArch64 assembly code for the calculation above:
ldr d0, B fsub d0, d0, d1 fadd d3, d1, d0
fmul d0, d0, d0 fsqrt d0, d0 fdiv d3, d3, d2
ldr d1, A ldr d1, B str d3, X1
fmov d2, #4.0 fneg d1, d1 fsub d3, d1, d0
fmul d1, d1, d2 ldr d2, A fdiv d3, d3, d2
ldr d2, C fmov d3, #2.0 str d3, X2
fmul d1, d1, d2 fmul d2, d2, d3
DO loops. Fortran I is also notable for the introduction of the first control structure in a programming language: the DO counted loop.
This code repeatedly executes the lines between the DO command and the label 100 (excluded), with variable I taking successive values of 1, 2, …, N. The loop body is not supposed to change I, although some compilers tolerate it.
In addition to providing a concise notation for a common programming idiom, the DO notation can be compiled into efficient machine code. The original Fortran I compiler placed the loop test at the end of the loop body and performed limited forms of loop-invariant code motion and addressing strength reduction. Other optimizations that apply well to DO loops include loop unrolling and vectorization.
Control in Fortran. Besides DO loops, Fortran I supports GOTO commands that jump to a label unconditionally. For example, an infinite loop is written as follows:
The GOTO command also supports computed jumps, which are jumps to a label whose value is contained in a variable, as well as the ASSIGN command, which sets a variable to the value of a label. For example:
Fortran I supports conditional jumps via an unusual three-way arithmetic branch IF (X) L1, L2, L3, which branches to L1 if X < 0, to L2 if X = 0, and to L3 if X > 0. For example, the following code fragment sets Y to the absolute value of X:
The familiar IF command with a Boolean condition was introduced in Fortran IV (1961), along with Boolean operators and Boolean-valued comparisons .EQ. (equal), .LT. (less than), etc. For example, the computation of the absolute value of X can be written as follows:
IF can only be followed by a single command (except IF and DO), and there is no ELSE clause. More complex conditional commands must be expressed using IF…GOTO and labels:
Fortran 77 adds block-structured conditional statements IF…ELSE…END IF, so that the previous example can be written more clearly as
Fortran 99 adds block-structured counted loops DO…END DO and general loops DO WHILE…END DO.
Structured statements. In Fortran and most other programming languages, expressions such as (1 + X) * Y are formed by combining constants (here, 1) and variables (X, Y) using operators (+, *). The Algol programming language, introduced in 1960, extends this approach to commands, also called “statements” and written s below. Statements are built from basic commands such as
These basic commands can, then, be combined using control structures such as
begin s1; s2; … end
if be then s1 else s2
for i := e1 step e2 until e3 do s
while be do s
Here, e stands for an arithmetic expression and be for a Boolean expression. Blocks begin … end can also declare local variables and local labels. For example, the following block statement sets m to the largest value in the array a[1:n] and p to the position of that value in a.
A fresh perspective on programming languages. Unlike assembly language instructions or Fortran commands, Algol statements are recursive in nature and can be nested to any depth. This has led to new ways of describing programming languages that accommodate this recursive nature and emphasize compositionality.
At the syntactic level, Algol was the first programming language to be defined using a formal grammar, written in Backus-Naur form. Here is the grammar for a simplified Algol-like language:
| Statements: s | ::= | x := e | |||
| ∣ | proc(e1, …, en) | ||||
| ∣ | begin s1; …; sn end | ||||
| ∣ | if be then s1 [else s2] | ||||
| ∣ | while be do s | ||||
| ∣ | for x := e1 step e2 until e3 do s | ||||
| Arithmetic expressions: e | ::= | c ∣ x ∣ e1 + e2 ∣ … | |||
| Boolean expressions: be | ::= | true ∣ false ∣ e1 < e2 ∣ … |
Consequently, Algol compilers were the first to use recursive or stack-based parsing algorithms.
At the semantic level, Algol popularized the idea that the meaning of a command is determined as a combination of the meanings of its subcommands. This idea, informal at first, was later made mathematically precise in the work on denotational semantics by Strachey, Scott, and others (see section 6.2).
Unstructured control. In addition to control structures, Algol also supports goto jumps to labels L that are attached to statements:
| Statements: s | ::= | … | |||||
| ∣ | L: s | statement labeled L | |||||
| ∣ | goto L ∣ go to L ∣ go L | jump to label L |
The goto spelling is used in the 1963 revised report on Algol, while the 1976 report uses go to, and many compilers accept go as well.
Each label has a scope, which is the nearest block enclosing the definition of the label. A goto statement can only jump to a label that is currently in scope, i.e. a label defined in the same block as the goto statement or in an enclosing block. Consequently, goto cannot jump into a block from outside this block.
Jump within the block ✔ begin
integer i;
L:...
goto L
end |
Jump out of the block ✔ begin
integer i;
... goto L ...
end;
L: ... |
Jump into a block ✘
goto L;
begin
integer i;
L:...
end |
Combining control structures and goto jumps in the style of Algol quickly became the preferred way to describe algorithms in textbooks and journals. As early as 1960, the Communications of the ACM, a journal that played an important role in the early days of computer science, mandated the use of Algol instead of flowcharts to publish new algorithms.
As an example of this Algol style, here is binary search in a sorted array a[1:n].
We find this combination of goto with control structures in many imperative and object-oriented languages: Algol 68, Pascal, Ada, Simula, PL/I, C, C++, C#, Perl, Go, … Imperative languages with only structured control and no goto statements are relatively few: Modula-2 (1980), Eiffel (1986), Modula-3 (1988), Python (1991), Java (1995), Rust (2012), Swift (2014).
The control structures introduced by Algol 60 (blocks, conditionals, counted loops, general loops) are found in most, if not all, of the imperative languages that followed. Many variants and extensions of these control structures have been proposed and incorporated into some languages.
Flavors of conditionals. Many languages provide an elif or elseif construct to facilitate the writing of nested if…then…else conditionals:
| if be1 then s1 elif be2 then s2 elif … else sn |
An alternative syntax for cascading Boolean tests is the cond construct of Lisp:
Case analysis on a value of integer type or enumerated type is provided by the case construct of Pascal (left), the switch construct of C and C-like languages (center), and the match construct of Python (right):
case grade of
'A' : s1
'B', 'C': s2
'D' : s3
'F' : s4
end | switch (grade) {
case 'A': s1; break;
case 'B':
case 'C': s2; break;
case 'D': s3; break;
case 'F': s4; break;
} | match grade:
case 'A' : s1
case 'B' | 'C': s2
case 'D' : s3
case 'F' : s4 |
Pattern matching, as found in most functional languages (Haskell, OCaml, SML, …) and some imperative languages (Rust, Swift, C#, …) extends case analysis with the ability to destructure data types and bind values to variables.
Dijkstra’s Guarded Command Language (a notation for program specification and refinement) has a non-deterministic selection construct that executes one of the commands s1, …, sn for which the corresponding guard be1, …, ben is true:
|
If several guards are true, any one of the corresponding commands may be executed. If no guards are true, the program aborts. A similar construct is used in the Occam language to describe channel-based communication.
Flavors of loops. The while loop tests the loop condition at the beginning of each iteration. Consequently, the loop body may not be executed at all if the condition is initially false. An alternative is to test the loop condition at the end of each iteration, so that the loop body is always executed at least once. This is written do…while in C-like languages and repeat…until in Pascal. The following program equivalences apply:
Note that repeat…until inverts the meaning of the loop condition, from “true means continue” to “true means stop”.
Sometimes, it is useful to test the loop condition in the middle of the loop body, so that part of the body is always executed before the condition is tested. This idiom is known as “a loop and a half”. The Forth language has a BEGIN…WHILE…REPEAT construct to express this pattern. In Ada, we can write
which is equivalent to s1; while be do begin s2; s1 end, provided that s1 contains no exit statements.
Other languages use unconditional loops with early exits for this purpose (see section 1.6).
Unconditional loops, which stop only when the loop body triggers an exit, are given special syntax in some languages: loop…end loop in Ada, for {…} in Go. Other languages use loops with trivial conditions, such as while true do or repeat…until false.
In PL/I and Algol 68, counted for loops can have additional while conditions. Algol 68 has a very general do loop that subsumes unconditional loops, while loops and for loops:
|
Any or all of the bracketed clauses can be omitted.
More modern languages have for loops that iterate not just over a range of numbers, but over any collection of values, such as an array, a list, or a generator (see section 4.2). In Python for example, this is written as
In Java, this would be written as
Experience in writing algorithms in Algol or Algol-style pseudocode shows that many uses of goto statements are to prematurely terminate the execution of a while or for loop, before the loop condition is false or the loop index reaches its final value. (This is the case for the binary search example on page ??.)
Many programming languages provide a command that exits from the enclosing loop and jumps to the program point that follows the loop, thus terminating the loop immediately. This command is written break in C, C++, Java, and Python; exit in Ada and Fortran 90; last in Perl; and leave in Forth. For example, here is a Java loop that sums numbers entered interactively, until a negative number is encountered:
Several of these languages provide another command that stops the current iteration of the enclosing loop and immediately starts the next iteration. This is written continue in C, C++, Java, and Python; cycle in Fortran 90; next in Perl; and again in Forth.
Python provides a way to distinguish whether a loop exits normally or by executing a break command: the else clause, which is executed only if the loop exits normally, but is skipped by break commands. For example:
Sometimes, it is desirable to terminate not the immediately enclosing loop, but an outer enclosing loop. In Bourne shell, the loop to terminate is identified by its relative position:
break N terminates the N enclosing loops.
In Ada, Java and Rust, the loop to terminate is identified by a label: each loop optionally carries a label, and break L terminates all loops up to and including the loop labeled L.
For example, the following Java code searches a matrix for a positive element:
Likewise, the following Java code searches for a substring needle of length m in a string haystack of length n:
These multi-level exits, as they are called, play an important role in the study of the expressiveness of structured control, as shown in sections 2.4 and 2.6.
Conceptually, and sometimes practically as well, it is useful to exit from one or more enclosing blocks, not just loops, skipping the statements that follow the exit point in those blocks. Rust allows programmers to set a label L on a block, and exit this block with break L. In C and C++, blocks can be written as degenerate loops
do … while(0), but only a single level of break is supported.
WebAssembly provides a unified treatment of loops and blocks, which are collectively called “structured control instructions”. A br N instruction jumps to the end of the N+1-th enclosing structured control instruction if it is a block, or to the beginning of this structured control instruction if it is a loop. This idiom supports both multi-level break and multi-level continue.
The textbook Programming Languages: Design and Implementation by Pratt and Zelkowitz (2000) compares 12 programming languages from the standpoints of control structures and of data structures. It is also an excellent introduction to the programming language concepts used throughout this book.
Carpenter and Doran (1977) describe Turing’s ACE instruction set architecture and how it differs from von Neumann’s EDVAC architecture.
Backus (1998) tells how he and his IBM team designed Fortran I, II and III. Padua (2000) describes the Fortran I compiler, which was “the first demonstration that it is possible to automatically generate efficient machine code from high-level languages”.
Algol 60 never had a large user base, but it had an enormous influence on the programming languages we use today. As Speed (2000) writes humorously, it is “the greatest computer language you’ve never used and the grandaddy of the programming family tree”. Rutishauser (1967) (available online) gives a comprehensive description of Algol 60 along with historical notes.